class: center, middle, inverse, title-slide # Probability: Binomial Distribution --- ### Annoucements - Mid-term feedback in journals - Homework #1 due Friday at 9 am - attach both .RMD and .html files to submission on Canvas --- ## Last week... - Introduction to probability - Jargon (elementary events, sample space, conditional, independence) - Frequentist - probability == long run rate - Bayesian - start with prior belief, incorporate data - Back to frequentist --- The **binomial distribution** is the theoretical probability distribution appropriate when modeling the expected outcome, X, of N trials (or event sequences) that have the following characteristics: -- - The outcome on every trial is binary - also called a **Bernoulli trial** -- - The probability of the target outcome (usually called a “success”) is the same for all N trials - “with replacement” might be necessary -- - The trials are independent -- - The number of trials is fixed --- If these assumptions hold then X is a binomial random variable representing the expected number of successes over N trials, with expected success on each trial of `\(\theta\)` . <p>&nbsp;</p> A common and compact way of stating the same thing is: <p>&nbsp;</p> `$$\Huge X \sim B(N, \theta)$$` --- The probability distribution for X is defined by the following **probability mass function**: `$$\Large P(X|\theta,N) = \frac{N!}{X!(N-X)!}\theta^X(1-\theta)^{N-X}$$` The probability mass function tells us what to expect for any particular X in the sample space. <p>&nbsp;</p> All theoretical distributions have a mass function (if discrete) or a density function (if continuous). These are the defining equations that tells us the generating process for the behavior of X. ??? A common way to write the binomial mass function is to think of `\(\theta\)` as the probability of success `\((p)\)` and `\(1-\theta\)` as the probability of failure `\((q)\)`. It becomes easier to write the function: $$ P(X|\theta,N) = \frac{N!}{X!(N-X)!}p^X(q)^{N-X}$$ --- `$$\Large P(X|\theta,N) = \frac{N!}{X!(N-X)!}\theta^X(1-\theta)^{N-X}$$` *** `\(\mathbf{P(X|\theta,N)}\)` is a conditional probability: the probability of X given `\(\theta\)` and `\(N\)`. - X is the number of successful trials over N independent trials, with the probability of success on any trial equal to `\(\theta\)`. - `\(\theta\)` and N are parameters of the binomial distribution. --- `$$\Large P(X|\theta,N) = \frac{N!}{X!(N-X)!}\theta^X(1-\theta)^{N-X}$$` *** `\(\mathbf{\theta^X(1-\theta)^{N-X}}\)` is the probability of any particular instance of X. - This is just a general form of the basic probability rule: `$$A \text{ and } B = P(A \cap B) = P(A)P(B)$$` Note that this form of the rule assumes *independent events*. --- For example, let's examine a sequence of 5 independent rolls of a die: `3 6 6 1 6` -- This can be represented in binomial form. First we have to choose the value that represents "success." Here, we'll use 6. `Not6 6 6 Not6 6` -- The probability of that particular sequence is then: `$$P(Not6)P(6)P(6)P(Not6)P(6)$$` -- `$$P(6)^3P(Not6)^2 = (\frac{1}{6})^3(\frac{5}{6})^2 = 0.0032$$` --- `$$\Large P(X|\theta,N) = \frac{N!}{X!(N-X)!}\theta^X(1-\theta)^{N-X}$$` *** But a specific sequence of independent outcomes is just one way we could have X successful trials out of N. - We need to know **how many possible ways** we could get X successes in N trials. The remaining part of the equation (the combination rule from probability theory, `\(_XC_N\)`), tells us how many different ways that can happen. `$$\Large \frac{N!}{X!(N-X)!}$$` --- Returning to our dice example, how many ways are there to roll a six 3 times out of 5? -- .pull-left[ `6 6 6 Not6 Not6` `6 6 Not6 6 Not6` `6 6 Not6 Not6 6` `6 Not6 6 6 Not6` `6 Not6 6 Not6 6` ] .pull-right[ `6 Not6 Not6 6 6` `Not6 6 6 6 Not6` `Not6 6 6 Not6 6` `Not6 6 Not6 6 6` `Not6 Not6 6 6 6` ] -- `$$\large \frac{5!}{3!(5-3)!} = \frac{5\times4\times3\times2\times1}{3\times2\times1(2\times1)}=10$$` --- Putting the pieces together: `$$\large P(X = \text{a }6, \text{three times}|\theta_6, N= 5)\\ = \frac{N!}{X!(N-X)!}\theta^X(1-\theta)^{N-X}\\= \frac{5!}{3!(5-3)!}(\frac{1}{6})^3(\frac{5}{6})^2\\ = (10)(.0032) \\ =.032$$` --- A note about notation: Many texts refer to the probability of success as `\(p\)` and the probability of not success (or failure) as `\(q\)`. In some ways, this makes the formula easier to understand: `$$P(X|p, N)= \frac{N!}{X!(N-X)!}p^Xq^{(N-X)}$$` --- What does the Law of Total Probability require to be true? <!-- --> ```r data.frame(num = 0:5, p = dbinom(x = 0:5, size = 5, prob = 1/6), three = as.factor(c(0,0,0,1,0,0))) %>% ggplot(aes(x=num, y=p, fill = three)) + geom_bar(stat="identity") + scale_x_continuous("Number of sixes (X) in five rolls (N)", breaks=c(0:5)) +scale_y_continuous("Probability")+ guides(fill = "none") + ggtitle("Binomial Probability Distribution") ``` ??? Independent rolls! --- Every probability distribution has an **expected value** distribution. For the binomial distribution: `$$E(X) = N\theta$$` -- Each probability distribution also has a variance. For the binomial: `$$Var(X) = N\theta(1-\theta)$$` -- Importantly, this means our mean and variance are related in the binomial distribution, because they both depend on `\(\theta\)`. How are they related? -- If you have a discrete distribution with a small N, these estimates may not have a sensible meaning. Later we will use the variance to help us make statements about how confident we are with regard to the location of the mean. ??? Expected value = most likely result of the probability function, * the thing we would expect to happen if we have no other information than the parameters of the distribution. *the long run average over an infinite amount of trials or samplings Sensible mean = number of arms example --- .left-column[ The mean, .835, does not exist in the sample space, and rounding up to 1 and claiming that to be the most typical outcome is not quite right either. ] <!-- --> --- The **probability mass (density) function** allows us to answer other questions about the sample space that might be more important, or at least realistic. - mass = discrete - density = continuous -- I might want to know the value in the sample space at or below which a certain proportion of outcomes fall. This is a **percentile or quantile** question. - "Most (75%) of five dice rolls yield X or fewer 6's." -- I might want to know the proportion of outcomes in the sample space that fall at or below a particular outcome. This is a **cumulative proportion** question. - "What percentage of the time will my outcome be less than 3?" --- At or below what outcome in the sample space do .75 of the outcomes fall? <!-- --> --- What proportion of outcomes in the sample space that fall at or below a given outcome? .pull-left[ <!-- --> ] .pull-right[ <!-- --> ] --- In R, we can calculate the cumulative probability (X or lower), using the `pbinom` function. ```r # what is probability of rolling two or fewer 6's out of five rolls? pbinom(q = 2, size = 5, prob = 1/6) ``` ``` ## [1] 0.9645062 ``` --- The binomial is of interest beyond describing the behavior of dice and coins. Many practical outcomes might be best described by a binomial distribution. For example, suppose I give a 40-item multiple choice test, with each question having 4 options. * I am worried that students might do well by chance alone. I would not want to pass students in the class if they were just showing up for the exams and guessing for each question. * What are the parameters in the binomial distribution that will help me address this question? ??? `\(N = 40\)` s `\(\theta = .25\)` --- <!-- --> ??? I could use this distribution to help me decide if a given student is consistent with a guessing model. Nearly all of the outcomes expected for guessers fall below the minimum passing score (60%, D-, 24). --- How likely is it that a guesser would score above the threshold (60%) necessary to pass the class by the most minimal standards? $$P(24|.25, 40) + P(25|.25,40) + P(26|.25,40) + ... + P(40|.25, 40) $$ -- <!-- `$$1-P(X = 23|\theta = .25, N= 40)= \\ 1-\frac{23!}{23!(40-23)!}(.25)^{23}(1-.25)^{17}$$` --> ```r #Note the use of the Law of Total Probability here 1-pbinom(q = 23, size = 40, prob = .25) ``` ``` ## [1] 2.825967e-06 ``` --- Cumulatively, what proportion of guessers will fall below each score? <!-- --> ??? Seems safe to assume that, practically speaking, all guessers will fall below the minimally passing score. --- ###There’s always a but But, what assumptions are we making and what consequences will they have? -- * The outcome on every trial is binary (also called a Bernoulli trial) -- * The probability of the target outcome (usually called a "success") is the same for all N trials ("with replacement" might be necessary) -- * The trials are independent `\(P(A\cap B) = P(A|B)P(B)=P(A)P(B)\)` -- * The number of trials is fixed -- In probability and statistics, if the assumptions are wrong then inferences based on those assumptions could be wrong too, perhaps seriously so. --- > All models are wrong, but some models are useful. (G.E.P. Box) We might have viable alternative models: * **Geometric distribution:** Used if we are interested in the number of trials required for one "success" to occur * "how many times do I start my computer before it fails to start at all?" --- > All models are wrong, but some models are useful. (G.E.P. Box) We might have viable alternative models: * **Negative binomial distribution:** Used if we are interested in the number of successes in a series of repeated trials until a specified number of failures are seen * "What is the probability that a baseball player will get his 2nd hit on his 4th at-bat?" * "A child won't return from trick or treating until they get 5 full-size candy bars. What is the probability that they will have to visit 34 homes to get this?" --- > All models are wrong, but some models are useful. (G.E.P. Box) We might have viable alternative models: * **Poisson distribution:** Used when there's not a fixed number of trials but rather a fixed interval of time. * "What is the expected number of times a solider will be kicked in the head by a horse and die during this one year campaign?" --- .left-column[ .small[As N increases, the binomial becomes more normal in appearance. Because of the difficulties in calculating large factorials, there is a large-sample normal approximation to the binomial. The normal distribution is useful for a lot of other reasons too. ] ] 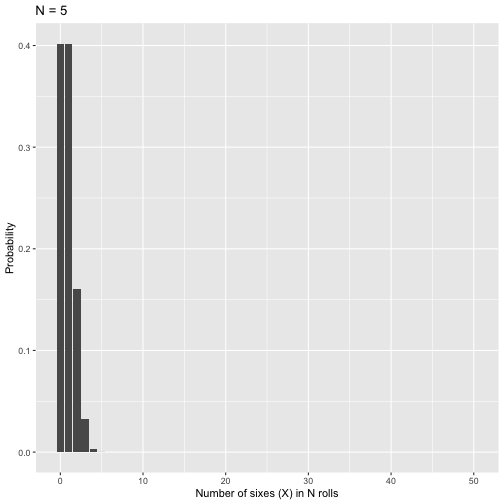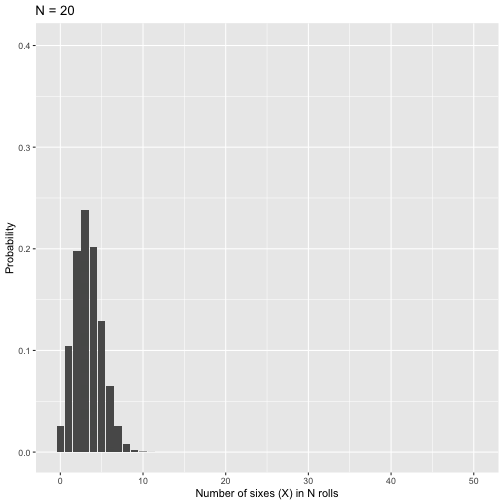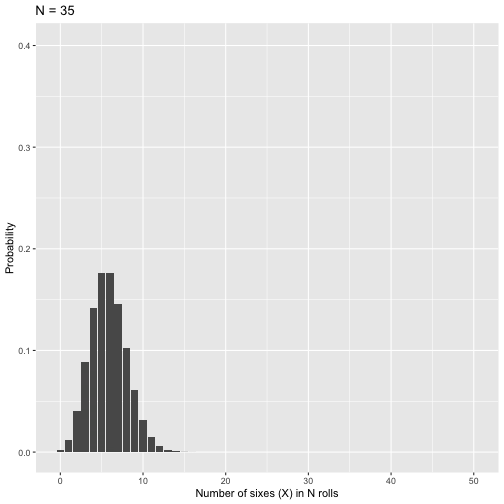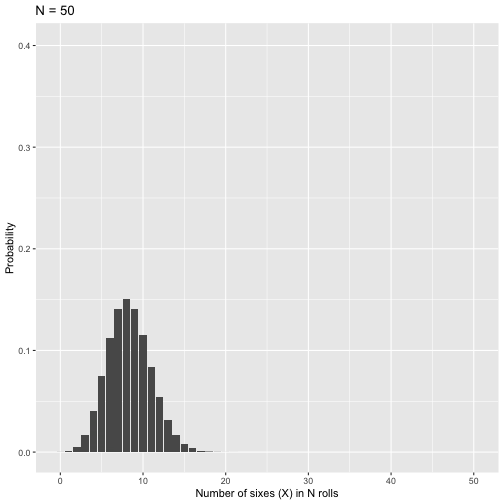<!-- --> --- class: inverse ## Next time... the normal distribution