Binomial Distributions

Annoucements

• Homework #1 due Friday at 9 am
  • attach both .RMD and .html files to submission on Canvas

# packages in this lecture
library(tidyverse)
library(gganimate)

Last week…

• Introduction to probability

• Jargon (elementary events, sample space, conditional, independence)

• Frequentist

  • probability == long run rate

• Bayesian

  • start with prior belief, incorporate data

• Back to frequentist

The binomial distribution is the theoretical probability distribution appropriate when modeling the expected outcome, X, of N trials (or event sequences) that have the following characteristics:

• The outcome on every trial is binary

  • also called a Bernoulli trial

• The probability of the target outcome (usually called a “success”) is the same for all N trials

  • “with replacement” might be necessary

• The trials are independent

• The number of trials is fixed

If these assumptions hold then X is a binomial random variable representing the expected number of successes over N trials, with expected success on each trial of \(\theta\) .

A common and compact way of stating the same thing is:

\[\large X \sim B(N, \theta)\]

The probability distribution for X is defined by the following probability mass function:

\[\large P(X|\theta,N) = \frac{N!}{X!(N-X)!}\theta^X(1-\theta)^{N-X}\]

The probability mass function tells us what to expect for any particular X in the sample space.

All theoretical distributions have a mass function (if discrete) or a density function (if continuous). These are the defining equations that tells us the generating process for the behavior of X.

A common way to write the binomial mass function is to think of \(\theta\) as the probability of success \((p)\) and \(1-\theta\) as the probability of failure \((q)\). It becomes easier to write the function:

\[ P(X|\theta,N) = \frac{N!}{X!(N-X)!}p^X(q)^{N-X}\]

\[P(X|\theta,N) = \frac{N!}{X!(N-X)!}\theta^X(1-\theta)^{N-X}\]

\(\mathbf{P(X|\theta,N)}\) is a conditional probability: the probability of X given \(\theta\) and \(N\).

• X is the number of successful trials over N independent trials, with the probability of success on any trial equal to \(\theta\).

• \(\theta\) and N are parameters of the binomial distribution.

\[\large P(X|\theta,N) = \frac{N!}{X!(N-X)!}\theta^X(1-\theta)^{N-X}\]

\(\mathbf{\theta^X(1-\theta)^{N-X}}\) is the probability of any particular instance of X.

This is just a general form of the basic probability rule:

\[A \text{ and } B = P(A \cap B) = P(A)P(B)\]

Note that this form of the rule assumes independent events.

For example, let’s examine a sequence of 5 independent rolls of a die:

3 6 6 1 6

This can be represented in binomial form. First we have to choose the value that represents “success.” Here, we’ll use 6.

Not6 6 6 Not6 6

The probability of that particular sequence is then:

\[P(Not6)P(6)P(6)P(Not6)P(6)\]

\[P(6)^3P(Not6)^2 = (\frac{1}{6})^3(\frac{5}{6})^2 = 0.0032\]

\[P(X|\theta,N) = \frac{N!}{X!(N-X)!}\theta^X(1-\theta)^{N-X}\]

But a specific sequence of independent outcomes is just one way we could have X successful trials out of N.

We need to know how many possible ways we could get X successes in N trials.

The remaining part of the equation (the combination rule from probability theory, \(_XC_N\)), tells us how many different ways that can happen.

\[\frac{N!}{X!(N-X)!}\]

Returning to our dice example, how many ways are there to roll a six 3 times out of 5?

6 6 6 Not6 Not6

6 6 Not6 6 Not6

6 6 Not6 Not6 6

6 Not6 6 6 Not6

6 Not6 6 Not6 6

6 Not6 Not6 6 6

Not6 6 6 6 Not6

Not6 6 6 Not6 6

Not6 6 Not6 6 6

Not6 Not6 6 6 6

\[\large \frac{5!}{3!(5-3)!} = \frac{5\times4\times3\times2\times1}{3\times2\times1(2\times1)}=10\]

Putting the pieces together:

\[\large P(X = \text{a }6, \text{three times}|\theta_6, N= 5)\\ = \frac{N!}{X!(N-X)!}\theta^X(1-\theta)^{N-X}\\= \frac{5!}{3!(5-3)!}(\frac{1}{6})^3(\frac{5}{6})^2\\ = (10)(.0032) \\ =.032\]

A note about notation:

Many texts refer to the probability of success as \(p\) and the probability of not success (or failure) as \(q\).

In some ways, this makes the formula easier to understand:

\[P(X|p, N)= \frac{N!}{X!(N-X)!}p^Xq^{(N-X)}\]

What does the Law of Total Probability require to be true?

Code

data.frame(num = 0:5, p = dbinom(x = 0:5, size = 5, prob = 1/6), three = as.factor(c(0,0,0,1,0,0))) %>% ggplot(aes(x=num, y=p, fill = three)) + geom_bar(stat="identity") + scale_x_continuous("Number of sixes (X) in five rolls (N)", breaks=c(0:5)) +scale_y_continuous("Probability")+ guides(fill = "none") + ggtitle("Binomial Probability Distribution")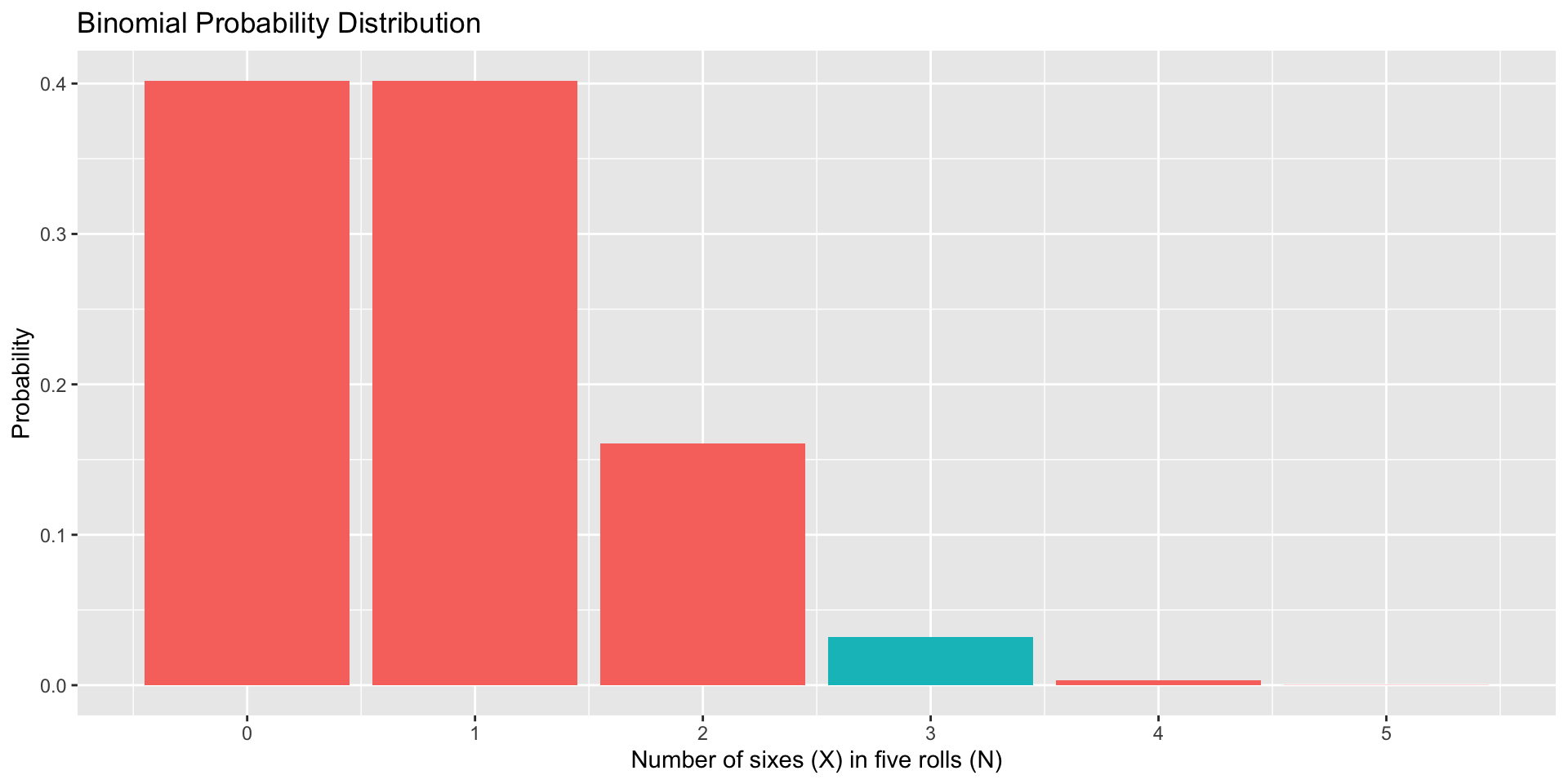

Independent rolls!

Every probability distribution has an expected value distribution.

For the binomial distribution:

\[E(X) = N\theta\]

Each probability distribution also has a variance. For the binomial:

\[Var(X) = N\theta(1-\theta)\]

Importantly, this means our mean and variance are related in the binomial distribution, because they both depend on \(\theta\). How are they related?

If you have a discrete distribution with a small N, these estimates may not have a sensible meaning.

Later we will use the variance to help us make statements about how confident we are with regard to the location of the mean.

Expected value = most likely result of the probability function, * the thing we would expect to happen if we have no other information than the parameters of the distribution. *the long run average over an infinite amount of trials or samplings

Sensible mean = number of arms example

The mean, .835, does not exist in the sample space, and rounding up to 1 and claiming that to be the most typical outcome is not quite right either.

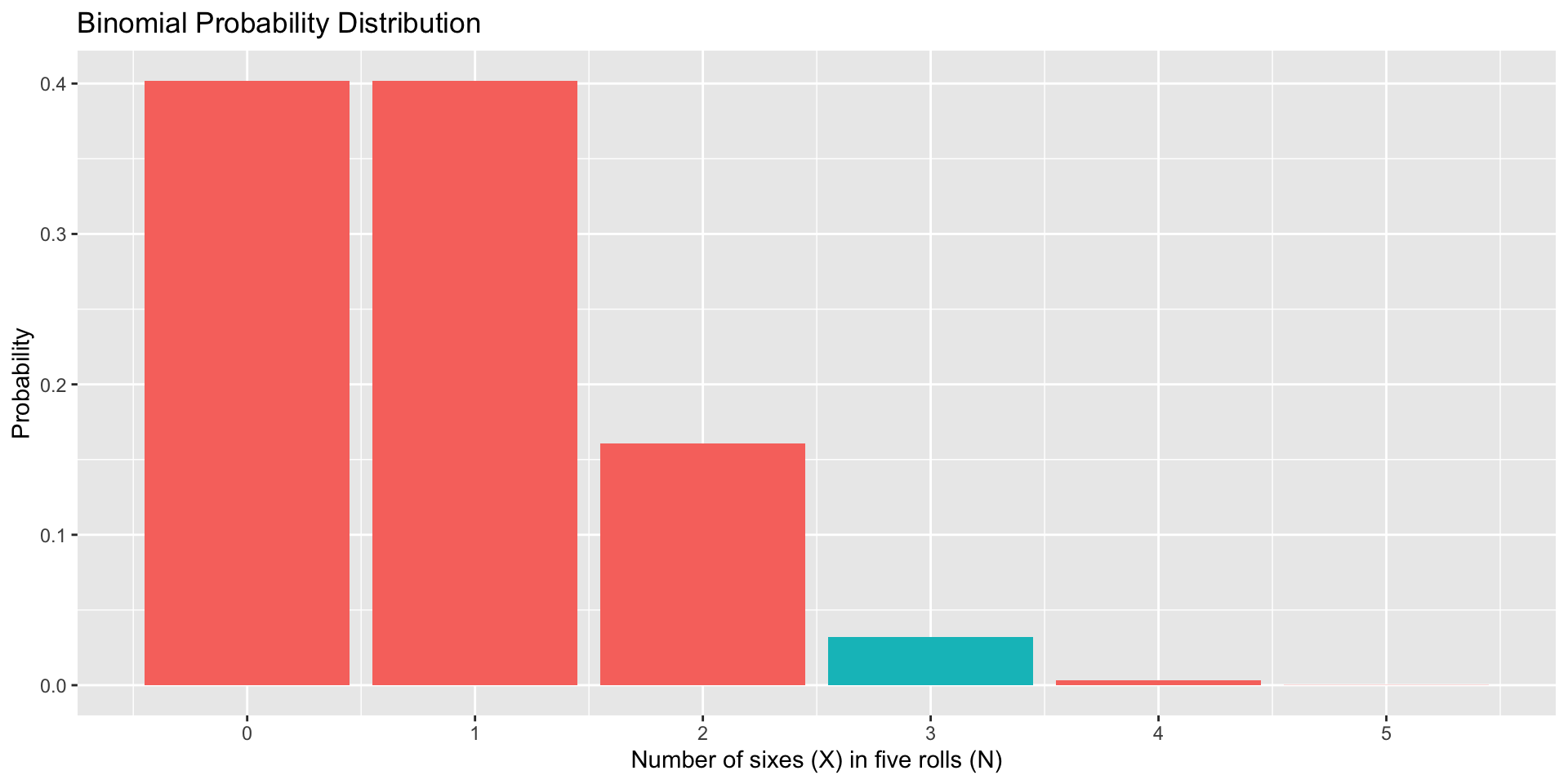
The probability mass (density) function allows us to answer other questions about the sample space that might be more important, or at least realistic.

• mass = discrete
• density = continuous

I might want to know the value in the sample space at or below which a certain proportion of outcomes fall. This is a percentile or quantile question.

• “Most (75%) of five dice rolls yield X or fewer 6’s.”

I might want to know the proportion of outcomes in the sample space that fall at or below a particular outcome. This is a cumulative proportion question. - “What percentage of the time will my outcome be less than 3?”

At or below what outcome in the sample space do .75 of the outcomes fall?

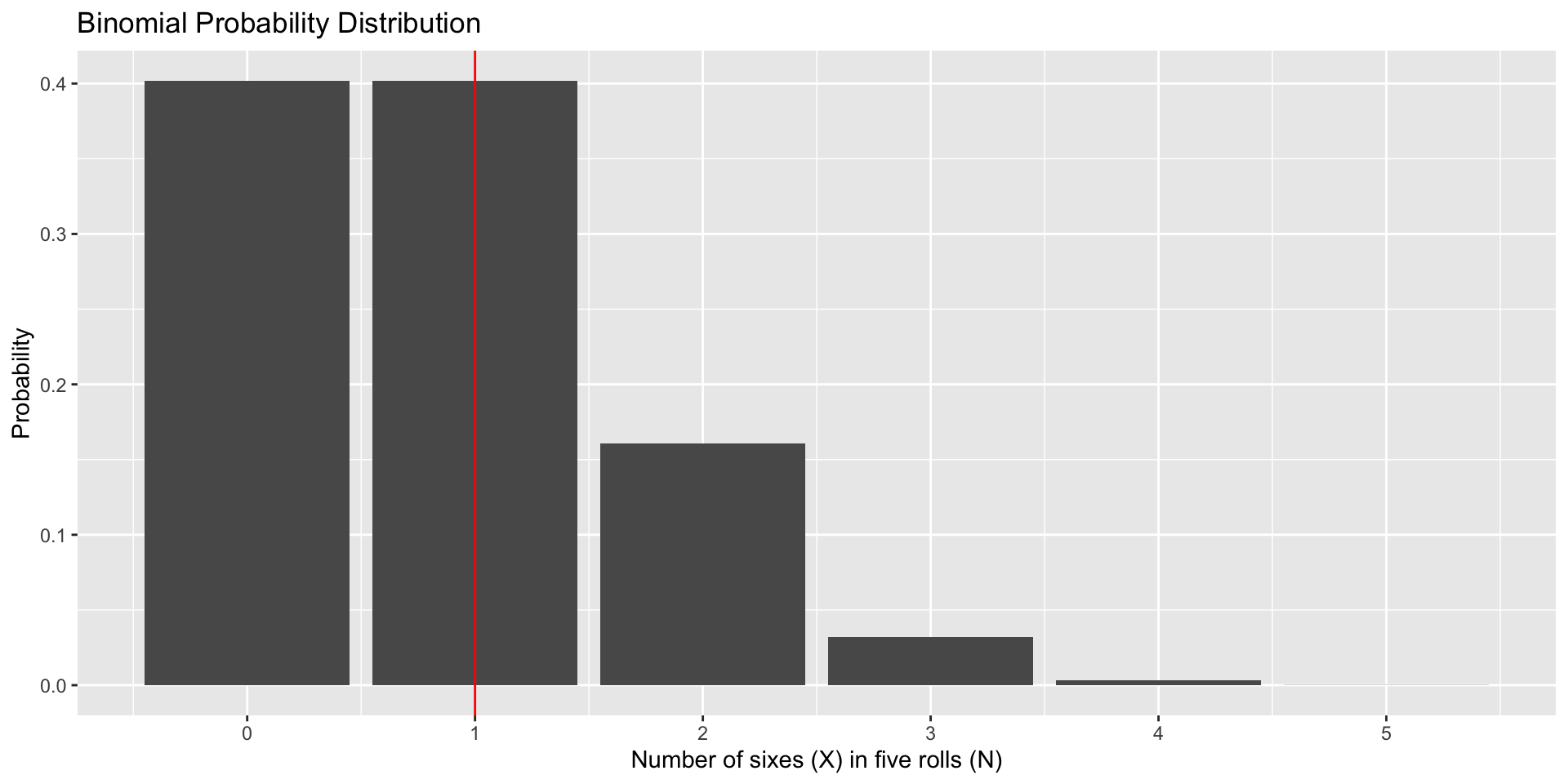
What proportion of outcomes in the sample space that fall at or below a given outcome?

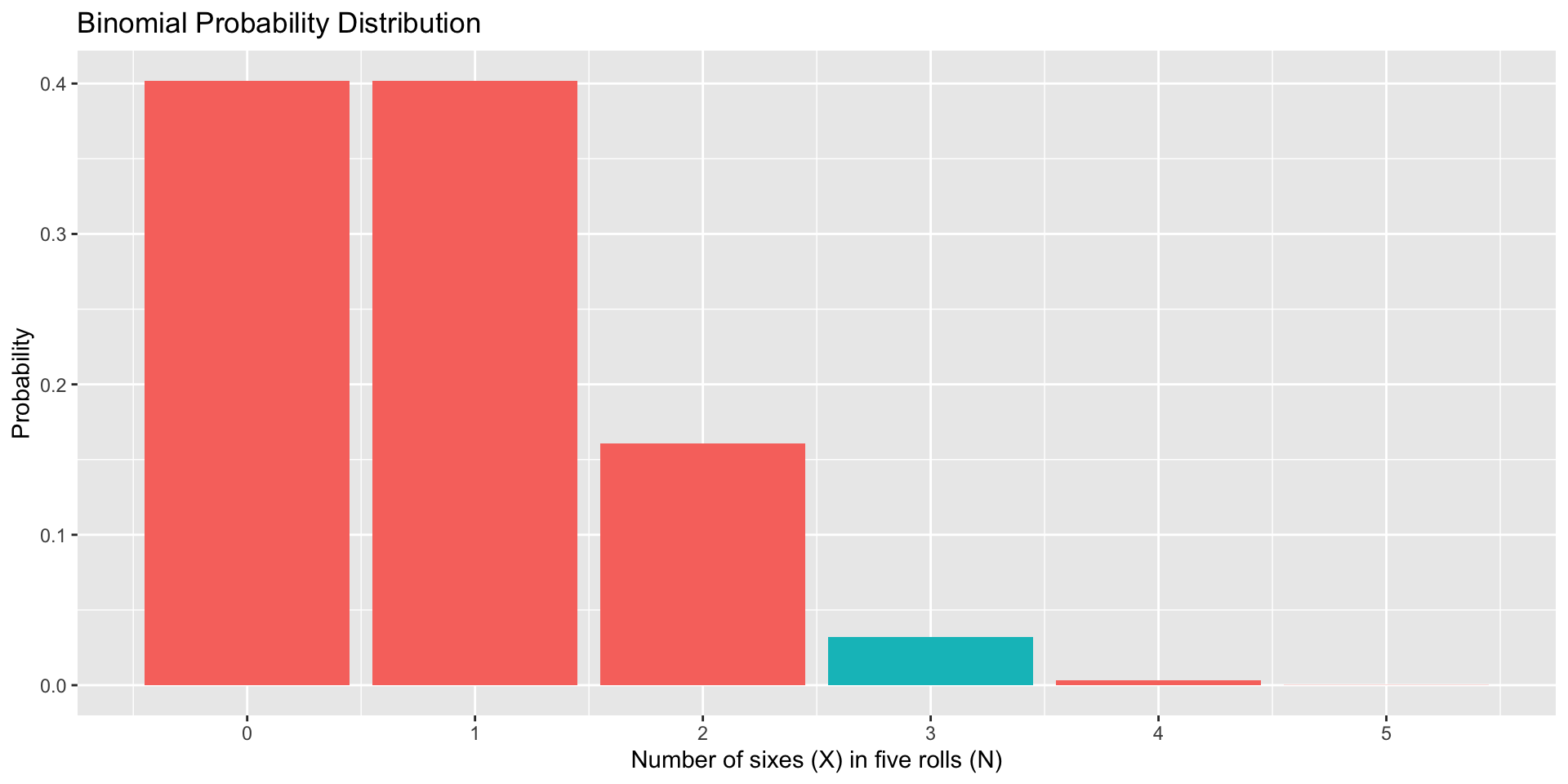
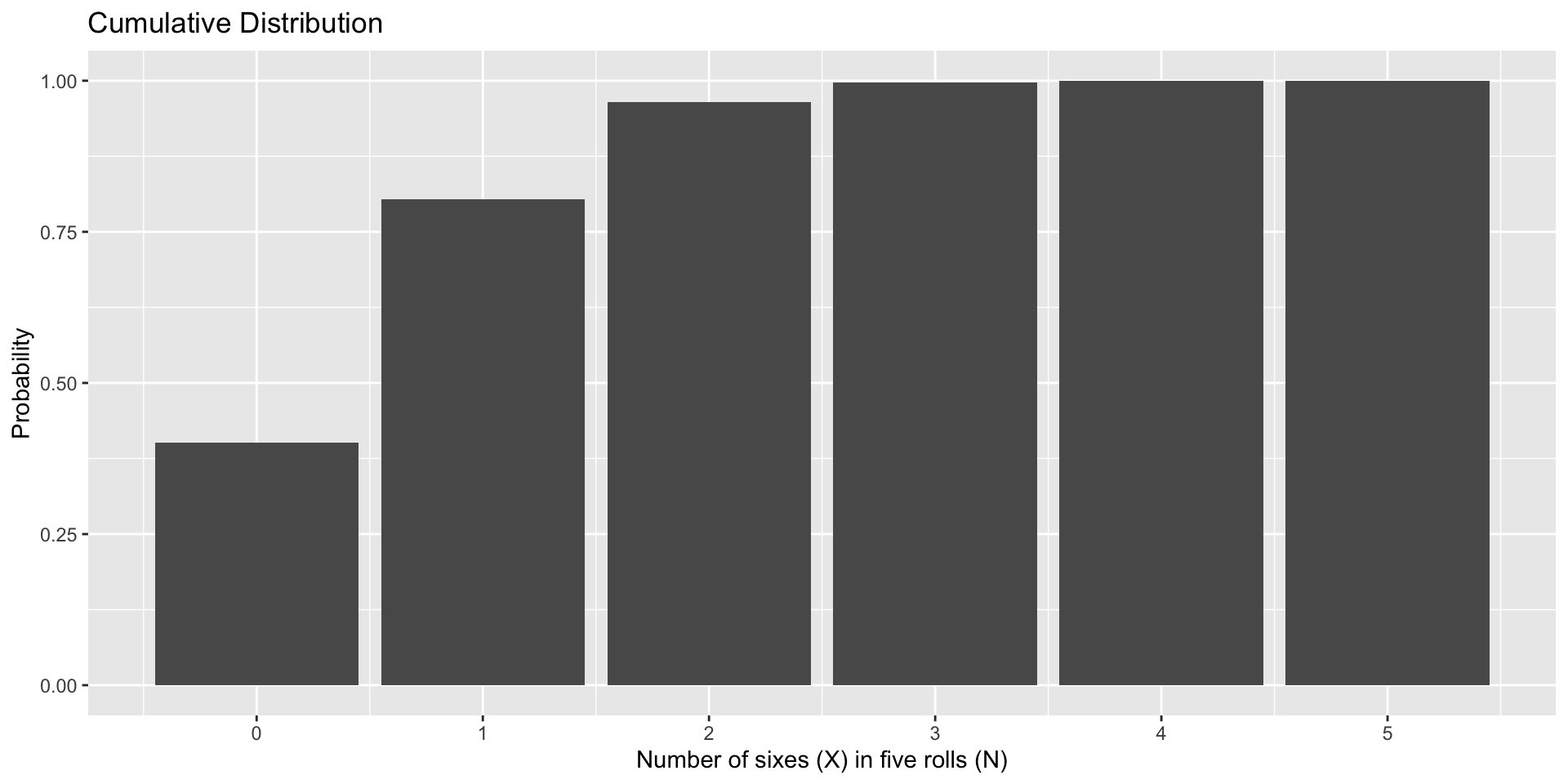
In R, we can calculate the cumulative probability (X or lower), using the pbinom function.

# what is probability of rolling two or fewer 6's out of five rolls?
pbinom(q = 2, size = 5, prob = 1/6)

[1] 0.9645062

The binomial is of interest beyond describing the behavior of dice and coins.

Many practical outcomes might be best described by a binomial distribution.

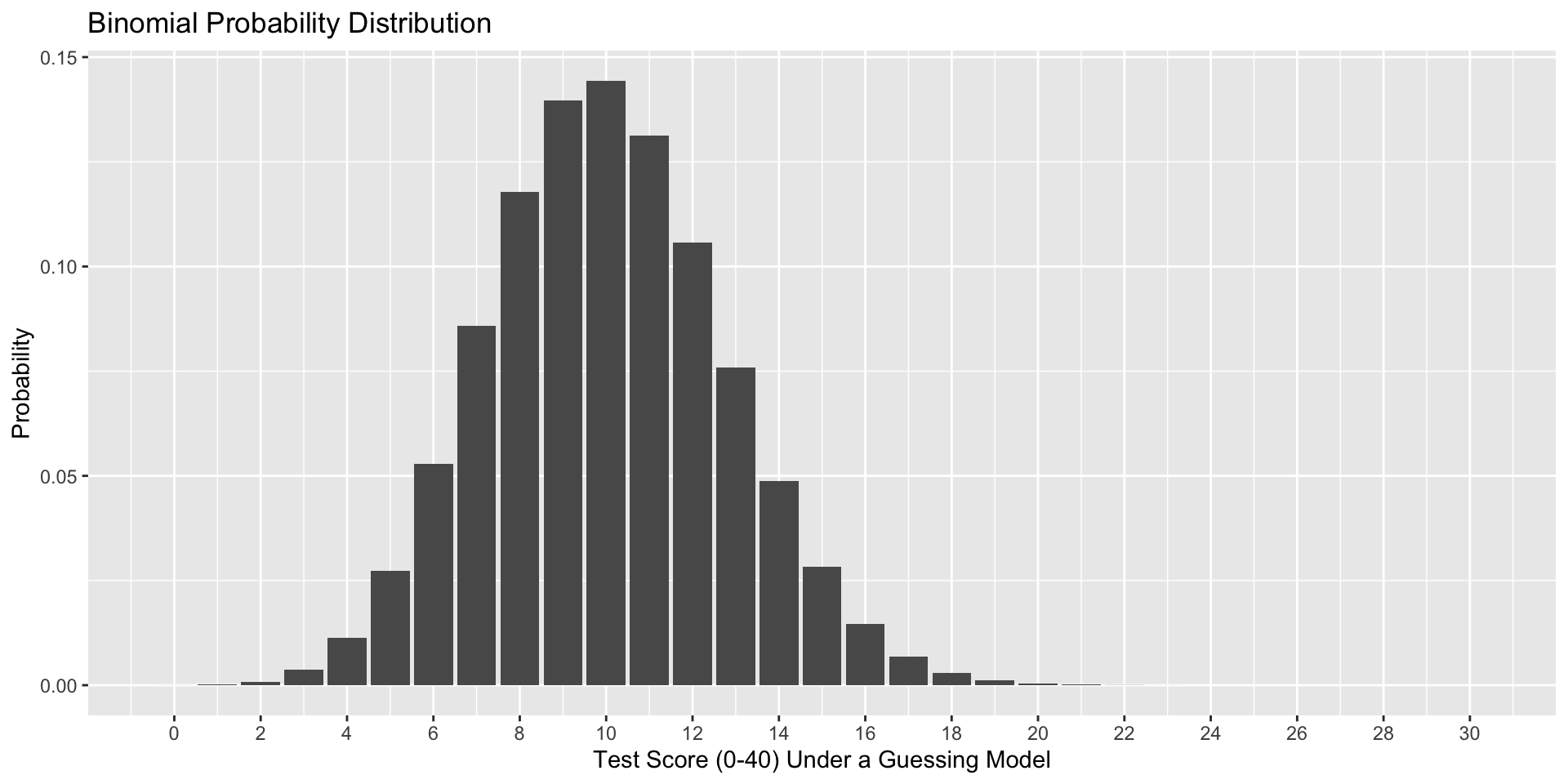
For example, suppose I give a 40-item multiple choice test, with each question having 4 options.

• I am worried that students might do well by chance alone. I would not want to pass students in the class if they were just showing up for the exams and guessing for each question.

• What are the parameters in the binomial distribution that will help me address this question?

\(N = 40\) s \(\theta = .25\)

I could use this distribution to help me decide if a given student is consistent with a guessing model.

Nearly all of the outcomes expected for guessers fall below the minimum passing score (60%, D-, 24).

How likely is it that a guesser would score above the threshold (60%) necessary to pass the class by the most minimal standards?

\[P(24|.25, 40) + P(25|.25,40) + P(26|.25,40) + ... + P(40|.25, 40) \]

#Note the use of the Law of Total Probability here
1-pbinom(q = 23, size = 40, prob = .25)

[1] 2.825967e-06

Cumulatively, what proportion of guessers will fall below each score?

Seems safe to assume that, practically speaking, all guessers will fall below the minimally passing score.

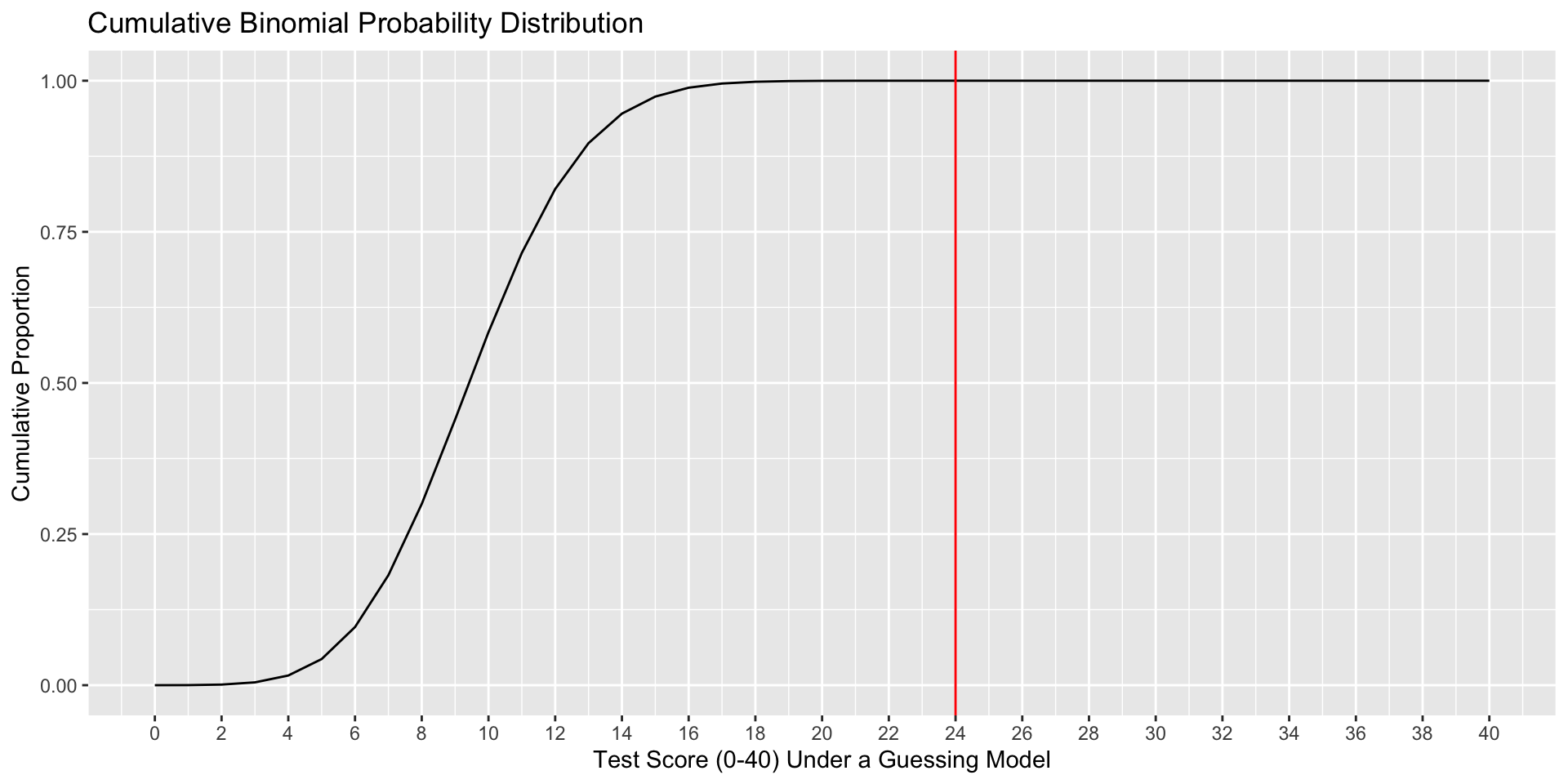
There’s always a but

But, what assumptions are we making and what consequences will they have?

• The outcome on every trial is binary (also called a Bernoulli trial)

• The probability of the target outcome (usually called a “success”) is the same for all N trials (“with replacement” might be necessary)

• The trials are independent \(P(A\cap B) = P(A|B)P(B)=P(A)P(B)\)

• The number of trials is fixed

In probability and statistics, if the assumptions are wrong then inferences based on those assumptions could be wrong too, perhaps seriously so.

We might have viable alternative models:

• Geometric distribution: Used if we are interested in the number of trials required for one “success” to occur
  • “how many times do I start my computer before it fails to start at all?”

We might have viable alternative models:

• Negative binomial distribution: Used if we are interested in the number of trials required for a specific number of “successes” to occur
  • “A child won’t return from trick or treating until they get 5 full-size candy bars. What is the probability that they will have to visit 34 homes to get this?”

We might have viable alternative models:

• Poisson distribution: Used when there’s not a fixed number of trials but rather a fixed interval of time.
  • “What is the expected number of times a solider will be kicked in the head by a horse and die during this one year campaign?”

As N increases…

As N increases, the binomial becomes more normal in appearance.

Because of the difficulties in calculating large factorials, there is a large-sample normal approximation to the binomial. The normal distribution is useful for a lot of other reasons too.

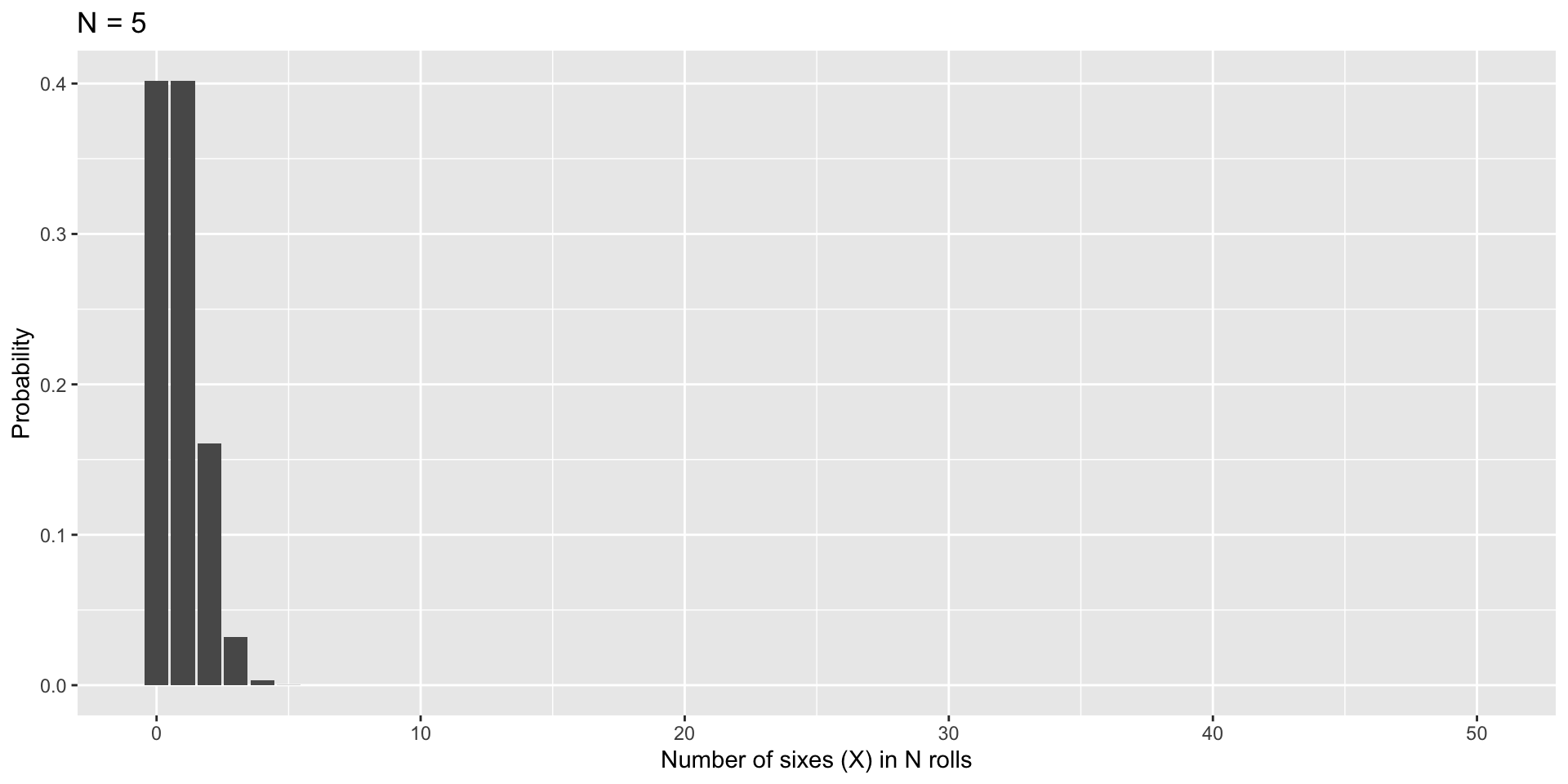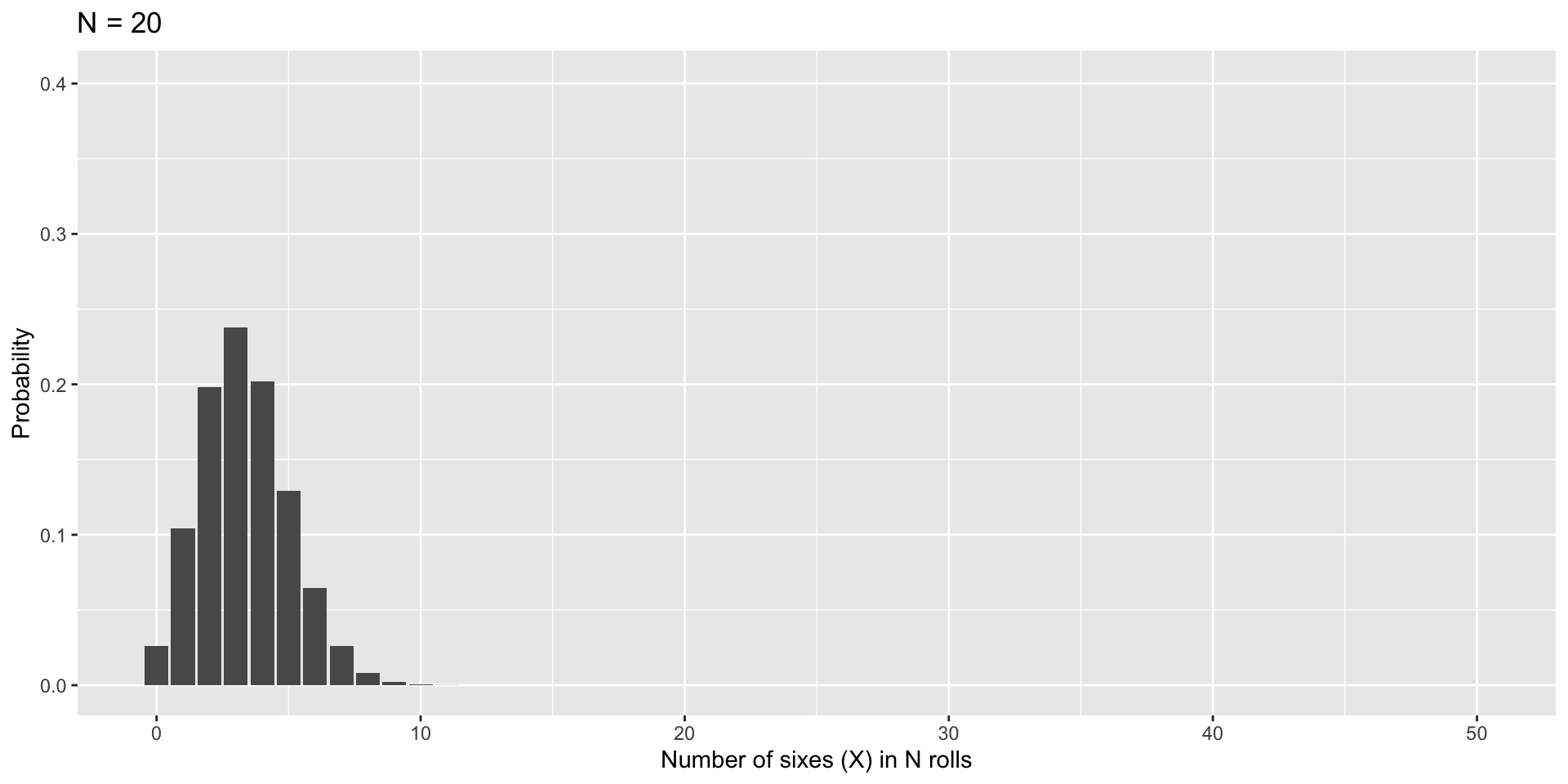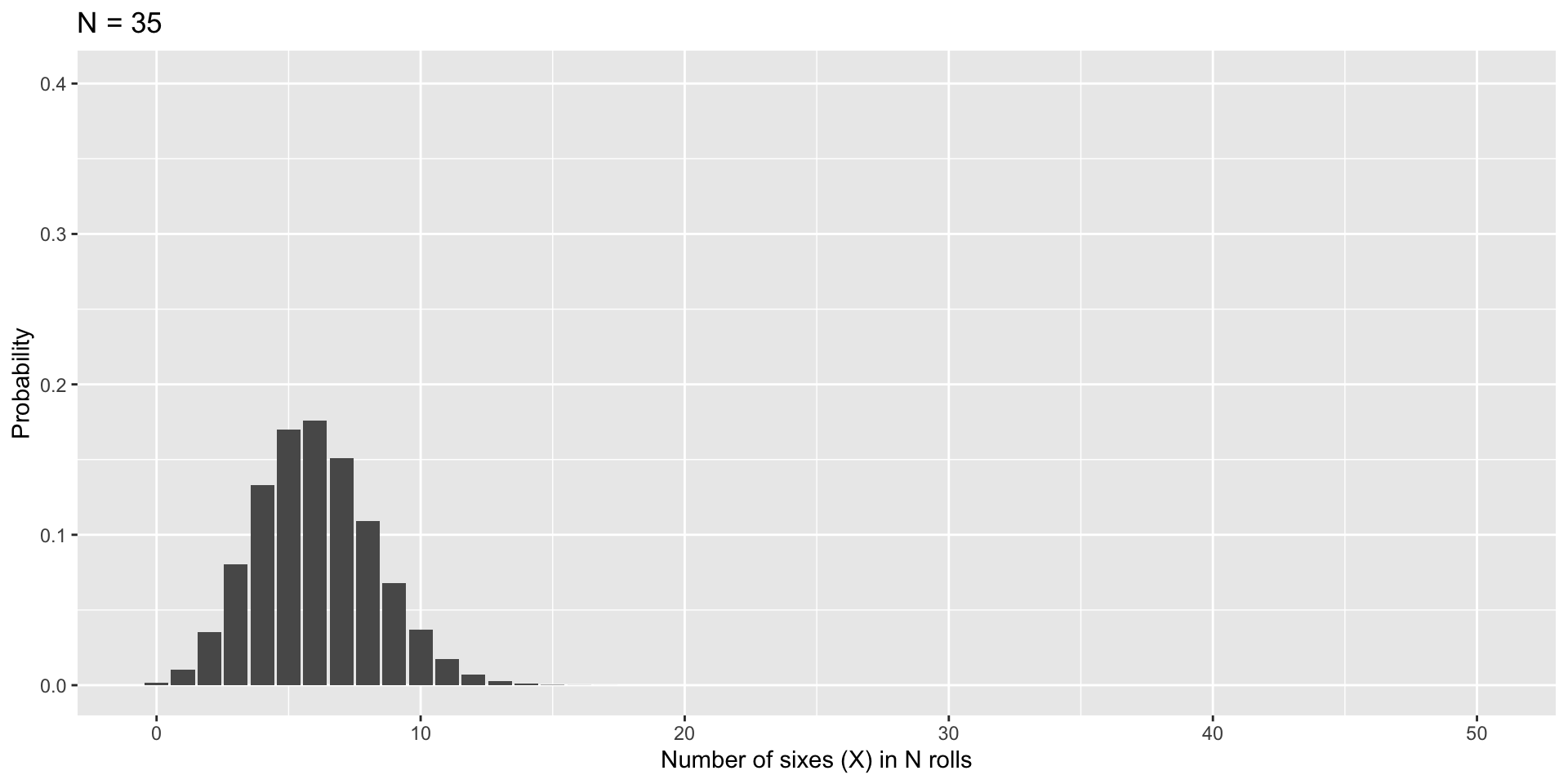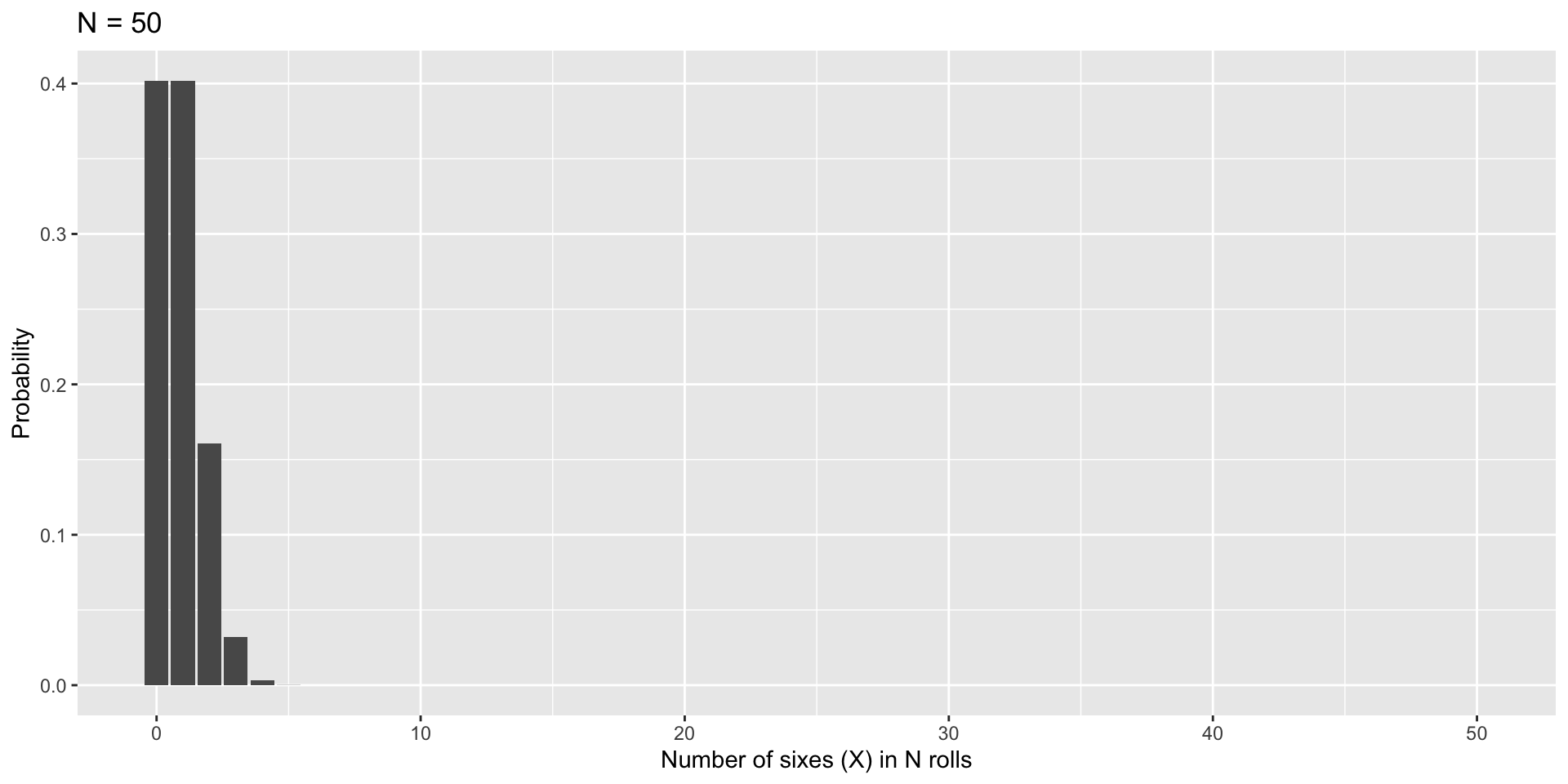
Next time…

the normal distribution