Correlations

Part 2

Recap

Correlations are:

Standardized covariances
- Range from -1 to 1
an effect size
- Measure of the strength of association between two continuous variables

Calculation:
- Sum the cross-product of deviation scores
- Divide by N-1
- Divide by the product of standard deviation scores

Example

Do Pulizters help newspapers keep readers? (Data from FiveThirtyEight).

library(fivethirtyeight)
data("pulitzer")
head(pulitzer)

            newspaper circ2004 circ2013 pctchg_circ num_finals1990_2003
1           USA Today  2192098  1674306         -24                   1
2 Wall Street Journal  2101017  2378827          13                  30
3      New York Times  1119027  1865318          67                  55
4   Los Angeles Times   983727   653868         -34                  44
5     Washington Post   760034   474767         -38                  52
6 New York Daily News   712671   516165         -28                   4
  num_finals2004_2014 num_finals1990_2014
1                   1                   2
2                  20                  50
3                  62                 117
4                  41                  85
5                  48                 100
6                   2                   6

x_var = pulitzer$pctchg_circ
y_var = pulitzer$num_finals2004_2014 
n = length(x_var)

x_d = x_var - mean(x_var)
y_d = y_var - mean(y_var)

describe(cbind(x_var, x_d, y_var, y_d), fast = T)

      vars  n   mean    sd     min   max range   se
x_var    1 50 -29.20 27.07 -100.00 67.00   167 3.83
x_d      2 50   0.00 27.07  -70.80 96.20   167 3.83
y_var    3 50   6.72 12.14    0.00 62.00    62 1.72
y_d      4 50   0.00 12.14   -6.72 55.28    62 1.72

# cross products
x_d*y_d

 [1]  -29.744  560.416 5317.936 -164.544 -363.264   -5.664  -48.384  -14.904
 [9] -156.704    2.016   17.856   -4.464  126.496   36.816 -189.904 -146.624
[17]   25.456  -10.944   27.176  -25.024   14.336    3.976    3.776  116.416
[25]   65.536  404.976   -4.864   -7.224 -208.624   13.056   43.896   32.096
[33]   12.096  186.816   50.976   56.056  263.376  119.616   59.136   99.456
[41]  -21.504   14.336  -61.824  -55.104  206.976  -46.784   40.176   99.456
[49]   40.176  -12.584

# sum of cross products (variation)
sum(x_d*y_d)

[1] 6482.2

# covariance
sum(x_d*y_d)/( n-1 )

[1] 132.2898

# correlation

( sum(x_d*y_d)/( n-1 ) ) / ( sd(x_var)*sd(y_var) )

[1] 0.4025279

cor(pulitzer$pctchg_circ,
    pulitzer$num_finals2004_2014)

[1] 0.4025279

cor.test(pulitzer$pctchg_circ,
    pulitzer$num_finals2004_2014)


    Pearson's product-moment correlation

data:  pulitzer$pctchg_circ and pulitzer$num_finals2004_2014
t = 3.0465, df = 48, p-value = 0.003755
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.1398493 0.6122747
sample estimates:
      cor 
0.4025279

Note: cor.test cannot handle a null hypothesis other than 0. You’ll have to calculate significance by hand if you’re interested in using another null.

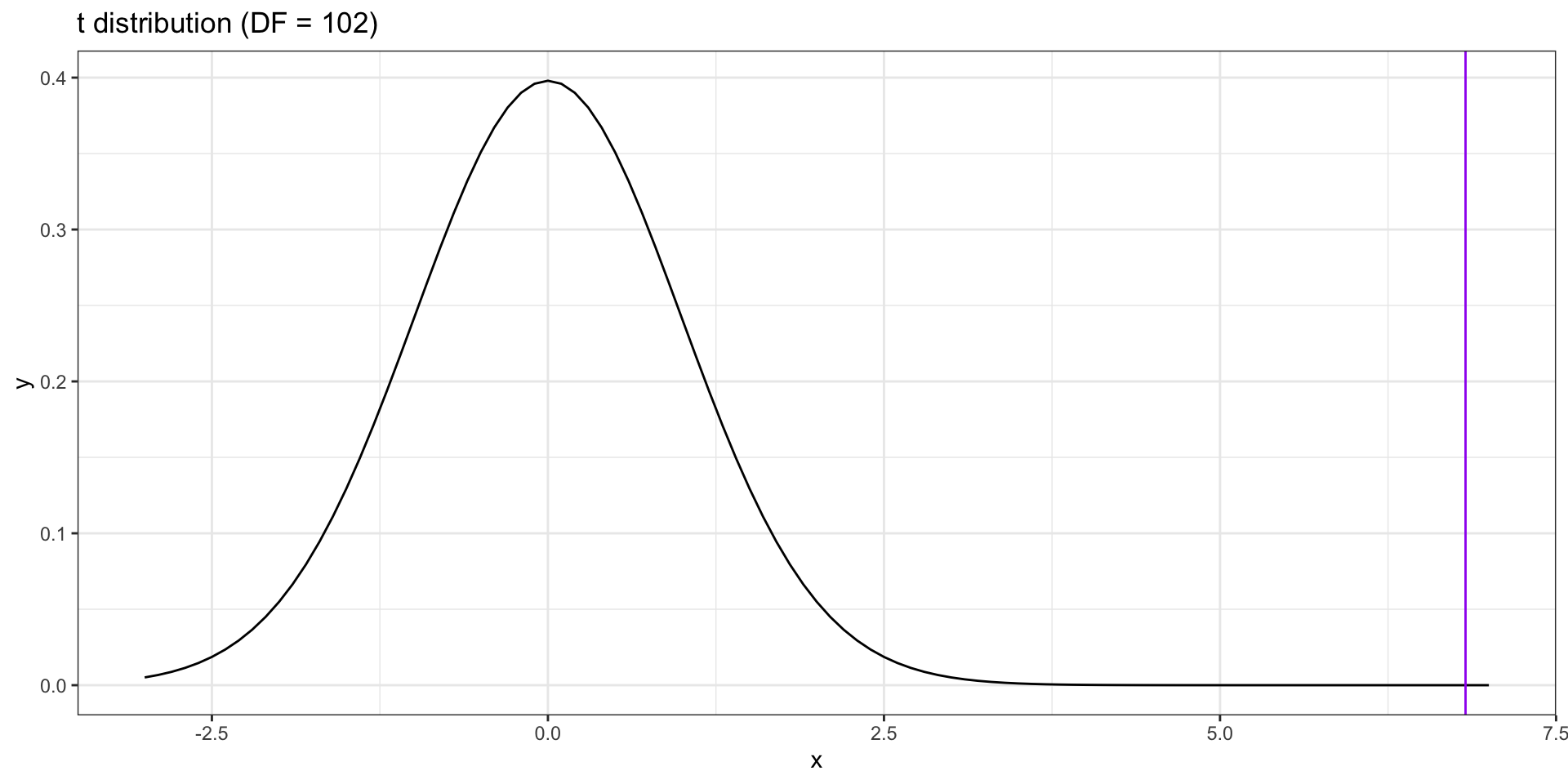
Recap: testing the significance of a correlation

If the null hypothesis is the nil hypothesis:

test significance using a t-distribution, where

\[t = \frac{r}{SE_r}\] \[SE_r = \sqrt{\frac{1-r^2}{N-2}}\] \[DF = N-2\]

If null hypothesis is not 0 \((\text{e.g., }H_0:\rho_{xy} = .40)\)

Transform statistic and null using Fisher’s r to Z

\[ z^{'} = {\frac{1}{2}}ln{\frac{1+r}{1-r}}\]

\[SE = \frac{1}{\sqrt{N-3}}\]

Example

In PSY 302, the correlation between midterm exam grades and final exam grades was .56. The class size was 104. Is this statistically significant?

Using t-method

\[SE_r = \sqrt{\frac{1-r^2}{N-2}} = \sqrt{\frac{1-.56^2}{104-2}} = 0.08\] \[t = \frac{r}{SE_r} = \frac{0.56}{0.08} = 6.83\]

Probability of getting a t statistic of 6.83 or greater is 0.

Code

library(tidyverse)
data.frame(x = c(-3,7)) %>%
  ggplot(aes(x = x)) +
  stat_function(fun = function(x) dt(x = x, df = N-2), geom = "line") +
  geom_vline(aes(xintercept = r/se), color = "purple") + 
  ggtitle("t distribution (DF = 102)")+
  theme_bw()

Example

In PSY 302, the correlation between midterm exam grades and final exam grades was .56. The class size was 104. Is this statistically significantly different from .40?

\[z^{'} = {\frac{1}{2}}ln{\frac{1+r}{1-r}}= {\frac{1}{2}}ln{\frac{1+0.56}{1-0.56}} = 0.63\] \[z^{'}_{H_0} = {\frac{1}{2}}ln{\frac{1+r}{1-r}}= {\frac{1}{2}}ln{\frac{1+0.4}{1-0.4}} = 0.42\] \[ SE_z = \frac{1}{\sqrt{104-3}} = 0.1\]

r = .56
N = 104
null = .40
zr = psych::fisherz(r)

[1] 0.6328332

znull = psych::fisherz(null)

[1] 0.4236489

se = 1/sqrt(N-3)

[1] 0.09950372

\[Z_{\text{statistic}} = \frac{z'-\mu}{SE_z}=\frac{0.63-0.42}{0.1} = 2.1\]

stat = (zr-znull)/se

[1] 2.102276

pnorm(stat, lower.tail = F)*2

[1] 0.03552913

Today

visualizing correlations
correlation matrices
reliability

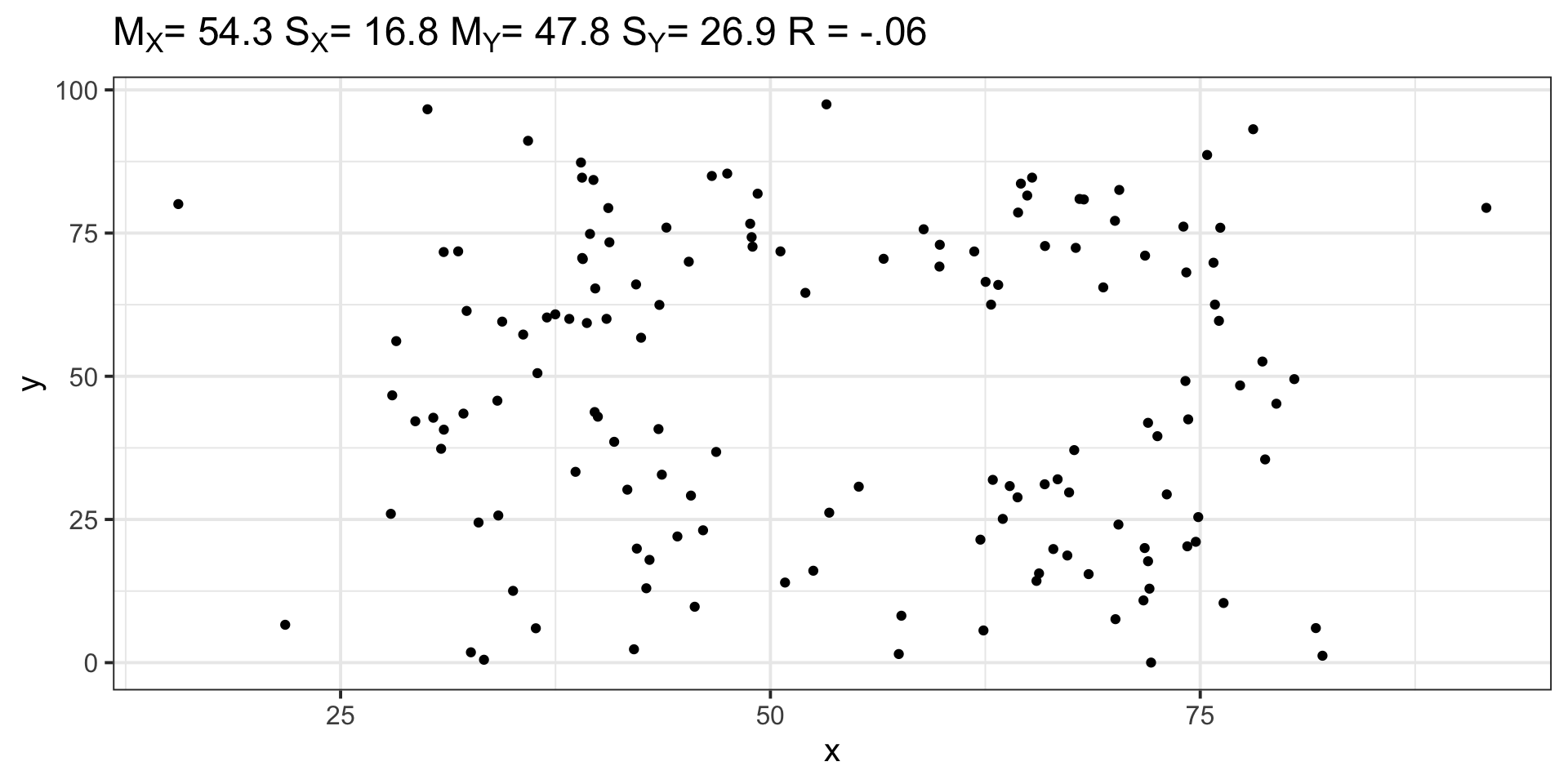
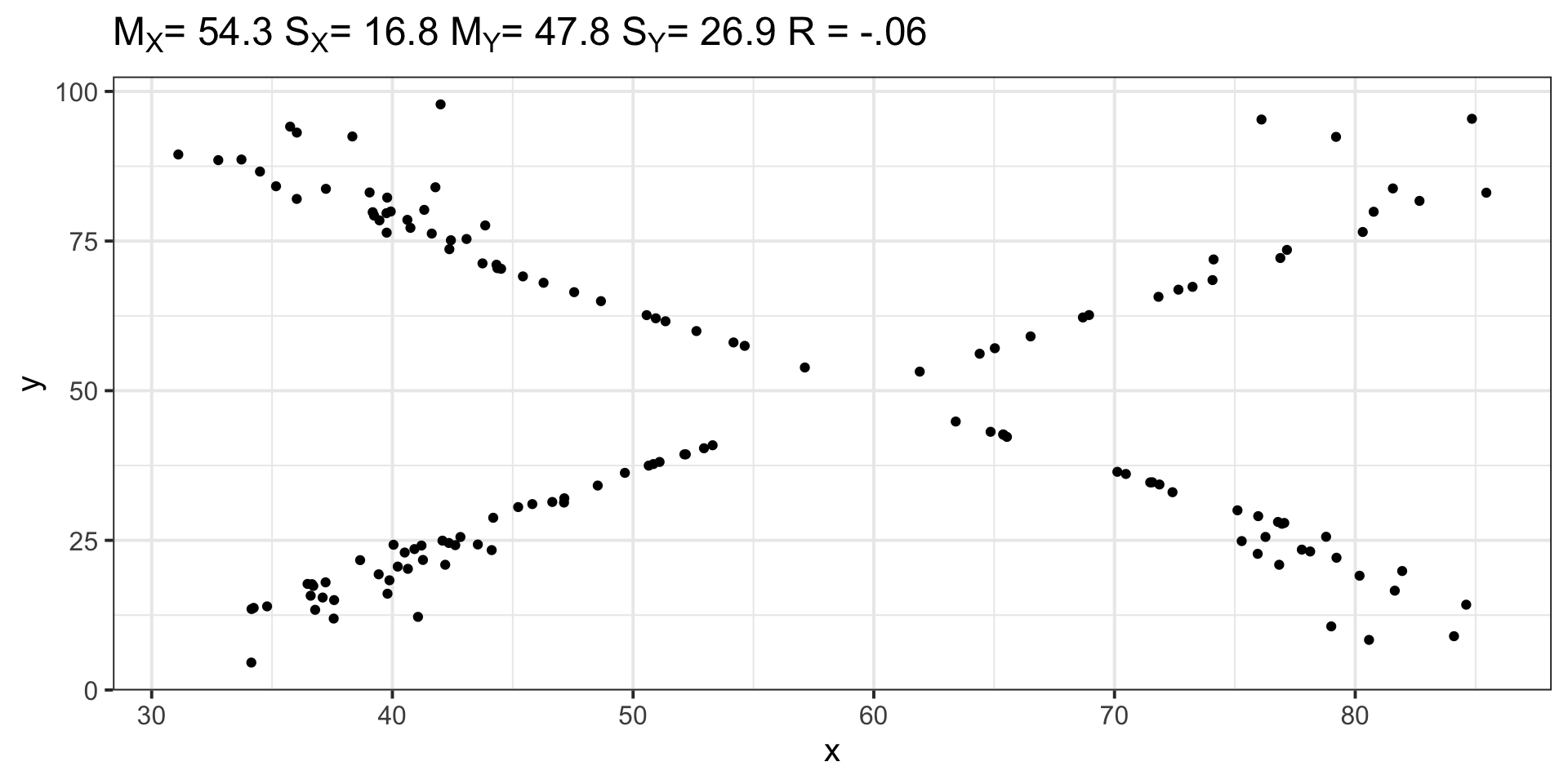
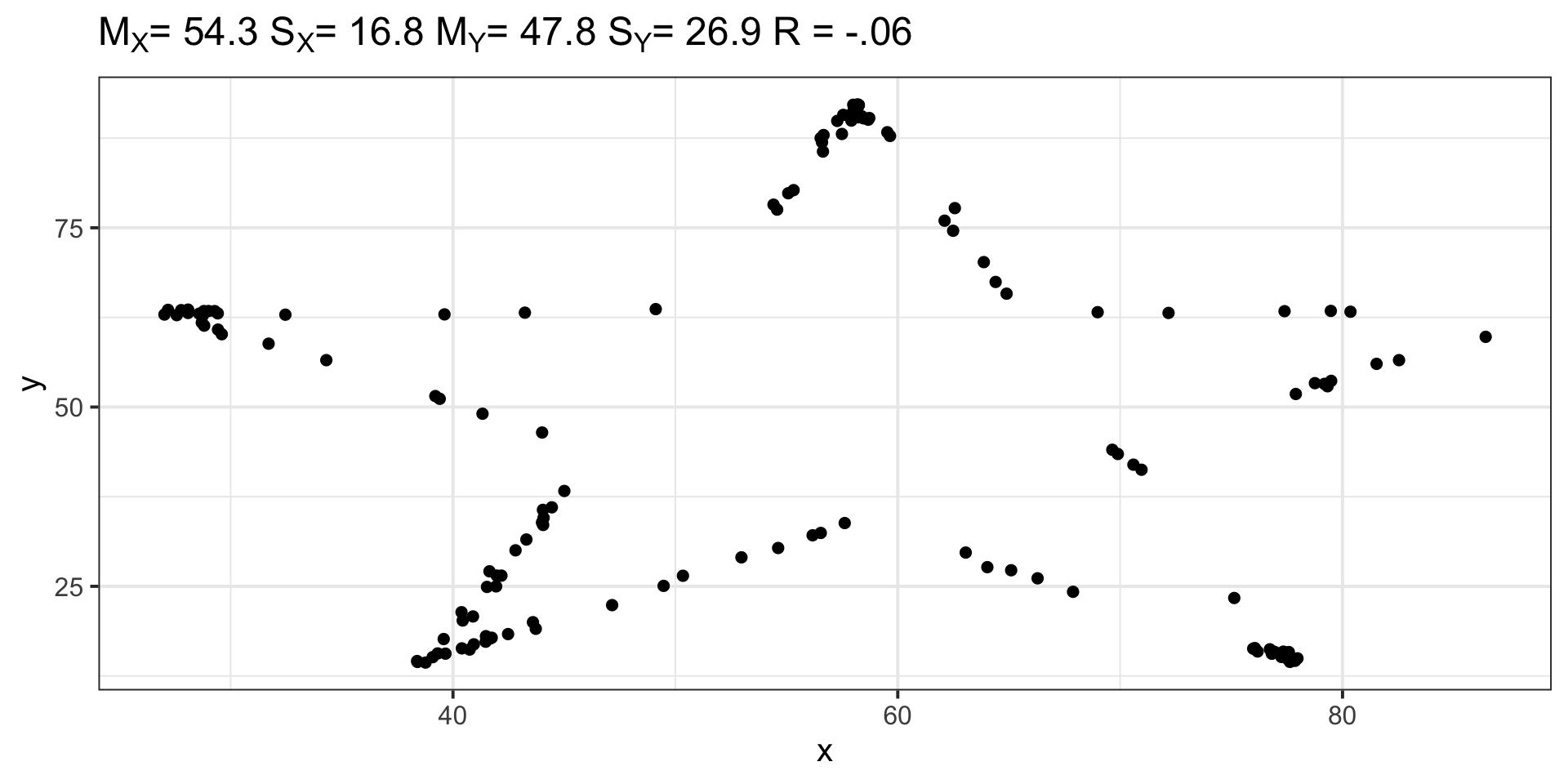
Visualizing correlations

For a single correlation, best practice is to visualize the relationship using a scatterplot. A best fit line is advised, as it can help clarify the strength and direction of the relationship.

http://guessthecorrelation.com/

Code

library(datasauRus)
datasaurus_dozen %>%
  filter(dataset == "away") %>%
  ggplot(aes(x = x, y = y)) +
  geom_point()+
  ggtitle(expression(paste(M[X], "= 54.3 ", S[X], "= 16.8 ", 
                           M[Y], "= 47.8 ", S[Y], "= 26.9 ",
                           "R = -.06"))) +
  theme_bw(base_size = 15)

Code

datasaurus_dozen %>%
  filter(dataset == "h_lines") %>%
  ggplot(aes(x = x, y = y)) +
  geom_point()+
  ggtitle(expression(paste(M[X], "= 54.3 ", S[X], "= 16.8 ", 
                           M[Y], "= 47.8 ", S[Y], "= 26.9 ",
                           "R = -.06"))) +
  theme_bw(base_size = 15)

Code

datasaurus_dozen %>%
  filter(dataset == "x_shape") %>%
  ggplot(aes(x = x, y = y)) +
  geom_point()+
  ggtitle(expression(paste(M[X], "= 54.3 ", S[X], "= 16.8 ", 
                           M[Y], "= 47.8 ", S[Y], "= 26.9 ",
                           "R = -.06"))) +
  theme_bw(base_size = 15)

Code

datasaurus_dozen %>%
  filter(dataset == "circle") %>%
  ggplot(aes(x = x, y = y)) +
  geom_point()+
  ggtitle(expression(paste(M[X], "= 54.3 ", S[X], "= 16.8 ", 
                           M[Y], "= 47.8 ", S[Y], "= 26.9 ",
                           "R = -.06"))) +
  theme_bw(base_size = 15)

Code

datasaurus_dozen %>%
  filter(dataset == "wide_lines") %>%
  ggplot(aes(x = x, y = y)) +
  geom_point()+
  ggtitle(expression(paste(M[X], "= 54.3 ", S[X], "= 16.8 ", 
                           M[Y], "= 47.8 ", S[Y], "= 26.9 ",
                           "R = -.06"))) +
  theme_bw(base_size = 15)

Code

datasaurus_dozen %>%
  filter(dataset == "bullseye") %>%
  ggplot(aes(x = x, y = y)) +
  geom_point()+
  ggtitle(expression(paste(M[X], "= 54.3 ", S[X], "= 16.8 ", 
                           M[Y], "= 47.8 ", S[Y], "= 26.9 ",
                           "R = -.06"))) +
  theme_bw(base_size = 15)

Code

datasaurus_dozen %>%
  filter(dataset == "star") %>%
  ggplot(aes(x = x, y = y)) +
  geom_point(size = 2)+
  ggtitle(expression(paste(M[X], "= 54.3 ", S[X], "= 16.8 ", 
                           M[Y], "= 47.8 ", S[Y], "= 26.9 ",
                           "R = -.06"))) +
  theme_bw(base_size = 15)

Code

datasaurus_dozen %>%
  filter(dataset == "dino") %>%
  ggplot(aes(x = x, y = y)) +
  geom_point(size = 2)+
  ggtitle(expression(paste(M[X], "= 54.3 ", S[X], "= 16.8 ", 
                           M[Y], "= 47.8 ", S[Y], "= 26.9 ",
                           "R = -.06"))) +
  theme_bw(base_size = 15)

Correlation matrices

Correlations are both a descriptive and an inferential statistic. As a descriptive statistic, they’re useful for understanding what’s going on in a larger dataset.

Like we use the summary() or describe() (psych) functions to examine our dataset before we run any infernetial tests, we should also look at the correlation matrix.

library(psych)
data(bfi)
head(bfi)

      A1 A2 A3 A4 A5 C1 C2 C3 C4 C5 E1 E2 E3 E4 E5 N1 N2 N3 N4 N5 O1 O2 O3 O4
61617  2  4  3  4  4  2  3  3  4  4  3  3  3  4  4  3  4  2  2  3  3  6  3  4
61618  2  4  5  2  5  5  4  4  3  4  1  1  6  4  3  3  3  3  5  5  4  2  4  3
61620  5  4  5  4  4  4  5  4  2  5  2  4  4  4  5  4  5  4  2  3  4  2  5  5
61621  4  4  6  5  5  4  4  3  5  5  5  3  4  4  4  2  5  2  4  1  3  3  4  3
61622  2  3  3  4  5  4  4  5  3  2  2  2  5  4  5  2  3  4  4  3  3  3  4  3
61623  6  6  5  6  5  6  6  6  1  3  2  1  6  5  6  3  5  2  2  3  4  3  5  6
      O5 gender education age
61617  3      1        NA  16
61618  3      2        NA  18
61620  2      2        NA  17
61621  5      2        NA  17
61622  3      1        NA  17
61623  1      2         3  21

cor(bfi)

          A1 A2 A3 A4 A5 C1 C2 C3 C4 C5 E1 E2 E3 E4 E5 N1 N2 N3 N4 N5 O1
A1         1 NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA
A2        NA  1 NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA
A3        NA NA  1 NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA
A4        NA NA NA  1 NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA
A5        NA NA NA NA  1 NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA
C1        NA NA NA NA NA  1 NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA
C2        NA NA NA NA NA NA  1 NA NA NA NA NA NA NA NA NA NA NA NA NA NA
C3        NA NA NA NA NA NA NA  1 NA NA NA NA NA NA NA NA NA NA NA NA NA
C4        NA NA NA NA NA NA NA NA  1 NA NA NA NA NA NA NA NA NA NA NA NA
C5        NA NA NA NA NA NA NA NA NA  1 NA NA NA NA NA NA NA NA NA NA NA
E1        NA NA NA NA NA NA NA NA NA NA  1 NA NA NA NA NA NA NA NA NA NA
E2        NA NA NA NA NA NA NA NA NA NA NA  1 NA NA NA NA NA NA NA NA NA
E3        NA NA NA NA NA NA NA NA NA NA NA NA  1 NA NA NA NA NA NA NA NA
E4        NA NA NA NA NA NA NA NA NA NA NA NA NA  1 NA NA NA NA NA NA NA
E5        NA NA NA NA NA NA NA NA NA NA NA NA NA NA  1 NA NA NA NA NA NA
N1        NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA  1 NA NA NA NA NA
N2        NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA  1 NA NA NA NA
N3        NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA  1 NA NA NA
N4        NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA  1 NA NA
N5        NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA  1 NA
O1        NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA  1
O2        NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA
O3        NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA
O4        NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA
O5        NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA
gender    NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA
education NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA
age       NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA
                   O2 O3 O4 O5     gender education         age
A1                 NA NA NA NA         NA        NA          NA
A2                 NA NA NA NA         NA        NA          NA
A3                 NA NA NA NA         NA        NA          NA
A4                 NA NA NA NA         NA        NA          NA
A5                 NA NA NA NA         NA        NA          NA
C1                 NA NA NA NA         NA        NA          NA
C2                 NA NA NA NA         NA        NA          NA
C3                 NA NA NA NA         NA        NA          NA
C4                 NA NA NA NA         NA        NA          NA
C5                 NA NA NA NA         NA        NA          NA
E1                 NA NA NA NA         NA        NA          NA
E2                 NA NA NA NA         NA        NA          NA
E3                 NA NA NA NA         NA        NA          NA
E4                 NA NA NA NA         NA        NA          NA
E5                 NA NA NA NA         NA        NA          NA
N1                 NA NA NA NA         NA        NA          NA
N2                 NA NA NA NA         NA        NA          NA
N3                 NA NA NA NA         NA        NA          NA
N4                 NA NA NA NA         NA        NA          NA
N5                 NA NA NA NA         NA        NA          NA
O1                 NA NA NA NA         NA        NA          NA
O2         1.00000000 NA NA NA 0.02694778        NA -0.04254386
O3                 NA  1 NA NA         NA        NA          NA
O4                 NA NA  1 NA         NA        NA          NA
O5                 NA NA NA  1         NA        NA          NA
gender     0.02694778 NA NA NA 1.00000000        NA  0.04770347
education          NA NA NA NA         NA         1          NA
age       -0.04254386 NA NA NA 0.04770347        NA  1.00000000

round(cor(bfi, use = "pairwise"),2)

             A1    A2    A3    A4    A5    C1    C2    C3    C4    C5    E1
A1         1.00 -0.34 -0.27 -0.15 -0.18  0.03  0.02 -0.02  0.13  0.05  0.11
A2        -0.34  1.00  0.49  0.34  0.39  0.09  0.14  0.19 -0.15 -0.12 -0.21
A3        -0.27  0.49  1.00  0.36  0.50  0.10  0.14  0.13 -0.12 -0.16 -0.21
A4        -0.15  0.34  0.36  1.00  0.31  0.09  0.23  0.13 -0.15 -0.24 -0.11
A5        -0.18  0.39  0.50  0.31  1.00  0.12  0.11  0.13 -0.13 -0.17 -0.25
C1         0.03  0.09  0.10  0.09  0.12  1.00  0.43  0.31 -0.34 -0.25 -0.02
C2         0.02  0.14  0.14  0.23  0.11  0.43  1.00  0.36 -0.38 -0.30  0.02
C3        -0.02  0.19  0.13  0.13  0.13  0.31  0.36  1.00 -0.34 -0.34  0.00
C4         0.13 -0.15 -0.12 -0.15 -0.13 -0.34 -0.38 -0.34  1.00  0.48  0.09
C5         0.05 -0.12 -0.16 -0.24 -0.17 -0.25 -0.30 -0.34  0.48  1.00  0.06
E1         0.11 -0.21 -0.21 -0.11 -0.25 -0.02  0.02  0.00  0.09  0.06  1.00
E2         0.09 -0.23 -0.29 -0.19 -0.33 -0.09 -0.06 -0.08  0.20  0.26  0.47
E3        -0.05  0.25  0.39  0.19  0.42  0.12  0.15  0.09 -0.08 -0.16 -0.33
E4        -0.06  0.28  0.38  0.30  0.47  0.14  0.12  0.09 -0.11 -0.20 -0.42
E5        -0.02  0.29  0.25  0.16  0.27  0.25  0.25  0.21 -0.24 -0.23 -0.30
N1         0.17 -0.09 -0.08 -0.10 -0.20 -0.07 -0.02 -0.07  0.22  0.21  0.02
N2         0.14 -0.05 -0.09 -0.14 -0.19 -0.04 -0.01 -0.06  0.16  0.25  0.01
N3         0.10 -0.04 -0.04 -0.07 -0.14 -0.03  0.00 -0.07  0.21  0.24  0.05
N4         0.05 -0.09 -0.13 -0.17 -0.20 -0.10 -0.05 -0.11  0.26  0.34  0.23
N5         0.02  0.02 -0.04 -0.01 -0.08 -0.05  0.05 -0.01  0.20  0.17  0.05
O1         0.01  0.13  0.15  0.06  0.16  0.17  0.16  0.09 -0.09 -0.08 -0.10
O2         0.08  0.02  0.00  0.04  0.00 -0.11 -0.04 -0.03  0.21  0.14  0.04
O3        -0.06  0.16  0.22  0.07  0.24  0.19  0.19  0.06 -0.08 -0.08 -0.22
O4        -0.08  0.09  0.04 -0.04  0.02  0.11  0.06  0.02  0.05  0.14  0.08
O5         0.11 -0.09 -0.05  0.02 -0.05 -0.12 -0.05 -0.01  0.20  0.06  0.10
gender    -0.16  0.18  0.14  0.13  0.10  0.01  0.07  0.05 -0.08 -0.09 -0.13
education -0.14  0.01  0.00 -0.02  0.01  0.03  0.00  0.05 -0.04  0.03  0.00
age       -0.16  0.11  0.07  0.14  0.13  0.08  0.02  0.07 -0.15 -0.09 -0.03
             E2    E3    E4    E5    N1    N2    N3    N4    N5    O1    O2
A1         0.09 -0.05 -0.06 -0.02  0.17  0.14  0.10  0.05  0.02  0.01  0.08
A2        -0.23  0.25  0.28  0.29 -0.09 -0.05 -0.04 -0.09  0.02  0.13  0.02
A3        -0.29  0.39  0.38  0.25 -0.08 -0.09 -0.04 -0.13 -0.04  0.15  0.00
A4        -0.19  0.19  0.30  0.16 -0.10 -0.14 -0.07 -0.17 -0.01  0.06  0.04
A5        -0.33  0.42  0.47  0.27 -0.20 -0.19 -0.14 -0.20 -0.08  0.16  0.00
C1        -0.09  0.12  0.14  0.25 -0.07 -0.04 -0.03 -0.10 -0.05  0.17 -0.11
C2        -0.06  0.15  0.12  0.25 -0.02 -0.01  0.00 -0.05  0.05  0.16 -0.04
C3        -0.08  0.09  0.09  0.21 -0.07 -0.06 -0.07 -0.11 -0.01  0.09 -0.03
C4         0.20 -0.08 -0.11 -0.24  0.22  0.16  0.21  0.26  0.20 -0.09  0.21
C5         0.26 -0.16 -0.20 -0.23  0.21  0.25  0.24  0.34  0.17 -0.08  0.14
E1         0.47 -0.33 -0.42 -0.30  0.02  0.01  0.05  0.23  0.05 -0.10  0.04
E2         1.00 -0.38 -0.51 -0.37  0.17  0.19  0.20  0.35  0.25 -0.16  0.08
E3        -0.38  1.00  0.42  0.38 -0.05 -0.07 -0.02 -0.15 -0.07  0.33 -0.07
E4        -0.51  0.42  1.00  0.32 -0.14 -0.14 -0.10 -0.29 -0.09  0.14  0.06
E5        -0.37  0.38  0.32  1.00  0.04  0.04 -0.06 -0.21 -0.13  0.30 -0.08
N1         0.17 -0.05 -0.14  0.04  1.00  0.71  0.56  0.40  0.38 -0.05  0.13
N2         0.19 -0.07 -0.14  0.04  0.71  1.00  0.55  0.39  0.35 -0.05  0.13
N3         0.20 -0.02 -0.10 -0.06  0.56  0.55  1.00  0.52  0.43 -0.03  0.11
N4         0.35 -0.15 -0.29 -0.21  0.40  0.39  0.52  1.00  0.40 -0.05  0.08
N5         0.25 -0.07 -0.09 -0.13  0.38  0.35  0.43  0.40  1.00 -0.12  0.20
O1        -0.16  0.33  0.14  0.30 -0.05 -0.05 -0.03 -0.05 -0.12  1.00 -0.21
O2         0.08 -0.07  0.06 -0.08  0.13  0.13  0.11  0.08  0.20 -0.21  1.00
O3        -0.23  0.39  0.21  0.29 -0.05 -0.03 -0.03 -0.06 -0.08  0.40 -0.26
O4         0.17  0.05 -0.10  0.00  0.08  0.13  0.18  0.21  0.11  0.18 -0.07
O5         0.08 -0.11  0.05 -0.11  0.11  0.04  0.06  0.04  0.14 -0.24  0.32
gender    -0.05  0.05  0.08  0.07  0.04  0.10  0.12  0.00  0.21 -0.10  0.03
education -0.01  0.00 -0.04  0.06 -0.05 -0.05 -0.05  0.01 -0.05  0.03 -0.09
age       -0.11  0.00 -0.01  0.11 -0.09 -0.10 -0.11 -0.03 -0.10  0.05 -0.04
             O3    O4    O5 gender education   age
A1        -0.06 -0.08  0.11  -0.16     -0.14 -0.16
A2         0.16  0.09 -0.09   0.18      0.01  0.11
A3         0.22  0.04 -0.05   0.14      0.00  0.07
A4         0.07 -0.04  0.02   0.13     -0.02  0.14
A5         0.24  0.02 -0.05   0.10      0.01  0.13
C1         0.19  0.11 -0.12   0.01      0.03  0.08
C2         0.19  0.06 -0.05   0.07      0.00  0.02
C3         0.06  0.02 -0.01   0.05      0.05  0.07
C4        -0.08  0.05  0.20  -0.08     -0.04 -0.15
C5        -0.08  0.14  0.06  -0.09      0.03 -0.09
E1        -0.22  0.08  0.10  -0.13      0.00 -0.03
E2        -0.23  0.17  0.08  -0.05     -0.01 -0.11
E3         0.39  0.05 -0.11   0.05      0.00  0.00
E4         0.21 -0.10  0.05   0.08     -0.04 -0.01
E5         0.29  0.00 -0.11   0.07      0.06  0.11
N1        -0.05  0.08  0.11   0.04     -0.05 -0.09
N2        -0.03  0.13  0.04   0.10     -0.05 -0.10
N3        -0.03  0.18  0.06   0.12     -0.05 -0.11
N4        -0.06  0.21  0.04   0.00      0.01 -0.03
N5        -0.08  0.11  0.14   0.21     -0.05 -0.10
O1         0.40  0.18 -0.24  -0.10      0.03  0.05
O2        -0.26 -0.07  0.32   0.03     -0.09 -0.04
O3         1.00  0.19 -0.31  -0.04      0.09  0.04
O4         0.19  1.00 -0.18   0.00      0.05  0.01
O5        -0.31 -0.18  1.00   0.02     -0.06 -0.10
gender    -0.04  0.00  0.02   1.00      0.01  0.05
education  0.09  0.05 -0.06   0.01      1.00  0.24
age        0.04  0.01 -0.10   0.05      0.24  1.00

round(cor(bfi, use = "complete"),2)

             A1    A2    A3    A4    A5    C1    C2    C3    C4    C5    E1
A1         1.00 -0.34 -0.26 -0.14 -0.19  0.02  0.01 -0.01  0.10  0.02  0.12
A2        -0.34  1.00  0.48  0.34  0.38  0.09  0.13  0.19 -0.14 -0.11 -0.24
A3        -0.26  0.48  1.00  0.38  0.50  0.10  0.14  0.13 -0.12 -0.15 -0.22
A4        -0.14  0.34  0.38  1.00  0.32  0.08  0.22  0.13 -0.16 -0.24 -0.14
A5        -0.19  0.38  0.50  0.32  1.00  0.12  0.11  0.13 -0.12 -0.16 -0.25
C1         0.02  0.09  0.10  0.08  0.12  1.00  0.43  0.32 -0.35 -0.25 -0.03
C2         0.01  0.13  0.14  0.22  0.11  0.43  1.00  0.36 -0.38 -0.30  0.02
C3        -0.01  0.19  0.13  0.13  0.13  0.32  0.36  1.00 -0.35 -0.35 -0.02
C4         0.10 -0.14 -0.12 -0.16 -0.12 -0.35 -0.38 -0.35  1.00  0.48  0.10
C5         0.02 -0.11 -0.15 -0.24 -0.16 -0.25 -0.30 -0.35  0.48  1.00  0.07
E1         0.12 -0.24 -0.22 -0.14 -0.25 -0.03  0.02 -0.02  0.10  0.07  1.00
E2         0.08 -0.24 -0.29 -0.20 -0.33 -0.10 -0.07 -0.09  0.21  0.26  0.47
E3        -0.04  0.25  0.38  0.20  0.41  0.13  0.15  0.10 -0.09 -0.17 -0.33
E4        -0.07  0.30  0.39  0.33  0.48  0.14  0.12  0.10 -0.12 -0.21 -0.42
E5        -0.02  0.30  0.26  0.16  0.27  0.26  0.25  0.22 -0.23 -0.24 -0.31
N1         0.16 -0.08 -0.07 -0.09 -0.19 -0.06 -0.02 -0.08  0.21  0.21  0.01
N2         0.13 -0.04 -0.08 -0.15 -0.19 -0.03  0.00 -0.06  0.15  0.24  0.01
N3         0.09 -0.02 -0.03 -0.07 -0.13 -0.01  0.01 -0.07  0.20  0.23  0.05
N4         0.04 -0.09 -0.13 -0.16 -0.21 -0.09 -0.04 -0.13  0.28  0.35  0.23
N5         0.01  0.02 -0.04  0.00 -0.08 -0.05  0.05 -0.04  0.21  0.18  0.04
O1         0.00  0.11  0.14  0.04  0.15  0.18  0.16  0.09 -0.10 -0.09 -0.10
O2         0.07  0.03  0.03  0.05  0.00 -0.13 -0.05 -0.03  0.21  0.12  0.06
O3        -0.06  0.15  0.22  0.04  0.22  0.19  0.18  0.06 -0.07 -0.07 -0.21
O4        -0.09  0.05  0.02 -0.06  0.00  0.08  0.03  0.00  0.07  0.14  0.08
O5         0.11 -0.08 -0.04  0.04 -0.04 -0.13 -0.06  0.00  0.18  0.05  0.09
gender    -0.17  0.21  0.16  0.13  0.11  0.00  0.06  0.04 -0.07 -0.09 -0.15
education -0.14  0.02  0.00 -0.02  0.02  0.04  0.01  0.06 -0.04  0.04  0.00
age       -0.14  0.09  0.04  0.11  0.10  0.08  0.00  0.05 -0.12 -0.07 -0.03
             E2    E3    E4    E5    N1    N2    N3    N4    N5    O1    O2
A1         0.08 -0.04 -0.07 -0.02  0.16  0.13  0.09  0.04  0.01  0.00  0.07
A2        -0.24  0.25  0.30  0.30 -0.08 -0.04 -0.02 -0.09  0.02  0.11  0.03
A3        -0.29  0.38  0.39  0.26 -0.07 -0.08 -0.03 -0.13 -0.04  0.14  0.03
A4        -0.20  0.20  0.33  0.16 -0.09 -0.15 -0.07 -0.16  0.00  0.04  0.05
A5        -0.33  0.41  0.48  0.27 -0.19 -0.19 -0.13 -0.21 -0.08  0.15  0.00
C1        -0.10  0.13  0.14  0.26 -0.06 -0.03 -0.01 -0.09 -0.05  0.18 -0.13
C2        -0.07  0.15  0.12  0.25 -0.02  0.00  0.01 -0.04  0.05  0.16 -0.05
C3        -0.09  0.10  0.10  0.22 -0.08 -0.06 -0.07 -0.13 -0.04  0.09 -0.03
C4         0.21 -0.09 -0.12 -0.23  0.21  0.15  0.20  0.28  0.21 -0.10  0.21
C5         0.26 -0.17 -0.21 -0.24  0.21  0.24  0.23  0.35  0.18 -0.09  0.12
E1         0.47 -0.33 -0.42 -0.31  0.01  0.01  0.05  0.23  0.04 -0.10  0.06
E2         1.00 -0.40 -0.52 -0.39  0.17  0.20  0.19  0.35  0.26 -0.16  0.08
E3        -0.40  1.00  0.43  0.40 -0.04 -0.06 -0.01 -0.15 -0.09  0.33 -0.07
E4        -0.52  0.43  1.00  0.33 -0.14 -0.15 -0.13 -0.31 -0.09  0.12  0.05
E5        -0.39  0.40  0.33  1.00  0.04  0.05 -0.06 -0.21 -0.14  0.29 -0.09
N1         0.17 -0.04 -0.14  0.04  1.00  0.71  0.57  0.41  0.38 -0.05  0.14
N2         0.20 -0.06 -0.15  0.05  0.71  1.00  0.55  0.39  0.35 -0.05  0.12
N3         0.19 -0.01 -0.13 -0.06  0.57  0.55  1.00  0.52  0.43 -0.05  0.11
N4         0.35 -0.15 -0.31 -0.21  0.41  0.39  0.52  1.00  0.40 -0.06  0.08
N5         0.26 -0.09 -0.09 -0.14  0.38  0.35  0.43  0.40  1.00 -0.15  0.20
O1        -0.16  0.33  0.12  0.29 -0.05 -0.05 -0.05 -0.06 -0.15  1.00 -0.23
O2         0.08 -0.07  0.05 -0.09  0.14  0.12  0.11  0.08  0.20 -0.23  1.00
O3        -0.24  0.41  0.21  0.30 -0.03 -0.02 -0.03 -0.06 -0.08  0.39 -0.29
O4         0.17  0.04 -0.10 -0.02  0.09  0.13  0.17  0.23  0.11  0.17 -0.08
O5         0.08 -0.13  0.04 -0.11  0.10  0.02  0.05  0.03  0.14 -0.25  0.33
gender    -0.08  0.05  0.11  0.08  0.04  0.09  0.11 -0.02  0.21 -0.11  0.04
education -0.01  0.01 -0.03  0.06 -0.04 -0.04 -0.04  0.01 -0.05  0.03 -0.10
age       -0.10 -0.02 -0.01  0.10 -0.07 -0.09 -0.11 -0.02 -0.10  0.05 -0.04
             O3    O4    O5 gender education   age
A1        -0.06 -0.09  0.11  -0.17     -0.14 -0.14
A2         0.15  0.05 -0.08   0.21      0.02  0.09
A3         0.22  0.02 -0.04   0.16      0.00  0.04
A4         0.04 -0.06  0.04   0.13     -0.02  0.11
A5         0.22  0.00 -0.04   0.11      0.02  0.10
C1         0.19  0.08 -0.13   0.00      0.04  0.08
C2         0.18  0.03 -0.06   0.06      0.01  0.00
C3         0.06  0.00  0.00   0.04      0.06  0.05
C4        -0.07  0.07  0.18  -0.07     -0.04 -0.12
C5        -0.07  0.14  0.05  -0.09      0.04 -0.07
E1        -0.21  0.08  0.09  -0.15      0.00 -0.03
E2        -0.24  0.17  0.08  -0.08     -0.01 -0.10
E3         0.41  0.04 -0.13   0.05      0.01 -0.02
E4         0.21 -0.10  0.04   0.11     -0.03 -0.01
E5         0.30 -0.02 -0.11   0.08      0.06  0.10
N1        -0.03  0.09  0.10   0.04     -0.04 -0.07
N2        -0.02  0.13  0.02   0.09     -0.04 -0.09
N3        -0.03  0.17  0.05   0.11     -0.04 -0.11
N4        -0.06  0.23  0.03  -0.02      0.01 -0.02
N5        -0.08  0.11  0.14   0.21     -0.05 -0.10
O1         0.39  0.17 -0.25  -0.11      0.03  0.05
O2        -0.29 -0.08  0.33   0.04     -0.10 -0.04
O3         1.00  0.17 -0.32  -0.04      0.10  0.02
O4         0.17  1.00 -0.18  -0.04      0.06  0.00
O5        -0.32 -0.18  1.00   0.04     -0.06 -0.08
gender    -0.04 -0.04  0.04   1.00      0.01  0.05
education  0.10  0.06 -0.06   0.01      1.00  0.25
age        0.02  0.00 -0.08   0.05      0.25  1.00

With pairwise deletion, different sets of cases contribute to different correlations. That maximizes the sample sizes, but can lead to problems if the data are missing for some systematic reason.

Listwise deletion (often referred to in R as use complete cases) doesn’t have the same issue of biasing correlations, but does result in smaller samples and potentially limited generalizability.

A good practice is comparing the different matrices; if the correlation values are very different, this suggests that the missingness that affects pairwise deletion is systematic.

round(cor(bfi, use = "pairwise")- cor(bfi, use = "complete"),2)

             A1    A2    A3    A4    A5    C1    C2    C3    C4    C5    E1
A1         0.00  0.00  0.00  0.00  0.00  0.01  0.00 -0.01  0.03  0.03 -0.01
A2         0.00  0.00  0.00 -0.01  0.01  0.00  0.01  0.01 -0.01 -0.01  0.03
A3         0.00  0.00  0.00 -0.02  0.00  0.00  0.00  0.00  0.00 -0.01  0.00
A4         0.00 -0.01 -0.02  0.00 -0.01  0.01  0.01  0.00  0.01  0.00  0.03
A5         0.00  0.01  0.00 -0.01  0.00  0.00  0.00  0.00 -0.01 -0.01  0.00
C1         0.01  0.00  0.00  0.01  0.00  0.00  0.00 -0.01  0.01  0.00  0.00
C2         0.00  0.01  0.00  0.01  0.00  0.00  0.00  0.00  0.00  0.00 -0.01
C3        -0.01  0.01  0.00  0.00  0.00 -0.01  0.00  0.00  0.02  0.01  0.02
C4         0.03 -0.01  0.00  0.01 -0.01  0.01  0.00  0.02  0.00 -0.01 -0.01
C5         0.03 -0.01 -0.01  0.00 -0.01  0.00  0.00  0.01 -0.01  0.00  0.00
E1        -0.01  0.03  0.00  0.03  0.00  0.00 -0.01  0.02 -0.01  0.00  0.00
E2         0.01  0.01  0.00  0.01  0.00  0.01  0.01  0.01 -0.01  0.00  0.00
E3         0.00  0.00  0.00 -0.01  0.00 -0.02  0.00 -0.02  0.01  0.01  0.01
E4         0.01 -0.02 -0.02 -0.03 -0.01  0.00  0.00 -0.01  0.01  0.01  0.00
E5         0.00  0.00 -0.01  0.00  0.00 -0.01  0.00  0.00  0.00  0.01  0.00
N1         0.01 -0.01 -0.02  0.00  0.00 -0.01  0.00  0.01  0.01  0.01  0.01
N2         0.01 -0.01  0.00  0.00  0.00 -0.01 -0.01  0.00  0.01  0.01  0.01
N3         0.01 -0.02 -0.01  0.00 -0.01 -0.02 -0.01  0.01  0.01  0.01  0.00
N4         0.01  0.00  0.00 -0.01  0.01 -0.01 -0.01  0.02 -0.02 -0.01  0.00
N5         0.01  0.00  0.00  0.00  0.00  0.00  0.00  0.02 -0.02 -0.01  0.01
O1         0.01  0.02  0.00  0.02  0.02 -0.01  0.01  0.00  0.01  0.01  0.00
O2         0.01 -0.02 -0.03 -0.01  0.00  0.02  0.01  0.00  0.00  0.02 -0.01
O3         0.00  0.02  0.01  0.03  0.02  0.00  0.01  0.01 -0.01 -0.01  0.00
O4         0.01  0.03  0.01  0.02  0.01  0.03  0.03  0.02 -0.02  0.00 -0.01
O5         0.01 -0.01 -0.01 -0.01 -0.01  0.01  0.00 -0.01  0.01  0.01  0.01
gender     0.01 -0.03 -0.02  0.00 -0.01  0.01  0.01  0.01 -0.01  0.00  0.02
education  0.00 -0.01 -0.01  0.00  0.00 -0.01 -0.01 -0.01  0.00 -0.01  0.00
age       -0.02  0.02  0.03  0.03  0.03  0.00  0.02  0.02 -0.03 -0.01  0.01
             E2    E3    E4    E5    N1    N2    N3    N4    N5    O1    O2
A1         0.01  0.00  0.01  0.00  0.01  0.01  0.01  0.01  0.01  0.01  0.01
A2         0.01  0.00 -0.02  0.00 -0.01 -0.01 -0.02  0.00  0.00  0.02 -0.02
A3         0.00  0.00 -0.02 -0.01 -0.02  0.00 -0.01  0.00  0.00  0.00 -0.03
A4         0.01 -0.01 -0.03  0.00  0.00  0.00  0.00 -0.01  0.00  0.02 -0.01
A5         0.00  0.00 -0.01  0.00  0.00  0.00 -0.01  0.01  0.00  0.02  0.00
C1         0.01 -0.02  0.00 -0.01 -0.01 -0.01 -0.02 -0.01  0.00 -0.01  0.02
C2         0.01  0.00  0.00  0.00  0.00 -0.01 -0.01 -0.01  0.00  0.01  0.01
C3         0.01 -0.02 -0.01  0.00  0.01  0.00  0.01  0.02  0.02  0.00  0.00
C4        -0.01  0.01  0.01  0.00  0.01  0.01  0.01 -0.02 -0.02  0.01  0.00
C5         0.00  0.01  0.01  0.01  0.01  0.01  0.01 -0.01 -0.01  0.01  0.02
E1         0.00  0.01  0.00  0.00  0.01  0.01  0.00  0.00  0.01  0.00 -0.01
E2         0.00  0.02  0.01  0.02  0.00  0.00  0.01 -0.01  0.00  0.00  0.00
E3         0.02  0.00 -0.01 -0.02 -0.01 -0.01 -0.01  0.01  0.01  0.00  0.01
E4         0.01 -0.01  0.00 -0.02  0.01  0.01  0.03  0.02  0.00  0.01  0.01
E5         0.02 -0.02 -0.02  0.00  0.00 -0.01  0.00  0.00  0.01  0.00  0.00
N1         0.00 -0.01  0.01  0.00  0.00  0.00 -0.01 -0.01 -0.01  0.00 -0.01
N2         0.00 -0.01  0.01 -0.01  0.00  0.00  0.00  0.00  0.00  0.00  0.00
N3         0.01 -0.01  0.03  0.00 -0.01  0.00  0.00  0.00  0.00  0.01  0.00
N4        -0.01  0.01  0.02  0.00 -0.01  0.00  0.00  0.00  0.00  0.01  0.00
N5         0.00  0.01  0.00  0.01 -0.01  0.00  0.00  0.00  0.00  0.03  0.00
O1         0.00  0.00  0.01  0.00  0.00  0.00  0.01  0.01  0.03  0.00  0.02
O2         0.00  0.01  0.01  0.00 -0.01  0.00  0.00  0.00  0.00  0.02  0.00
O3         0.02 -0.02  0.00  0.00 -0.02 -0.01  0.00  0.00  0.01  0.00  0.03
O4         0.00  0.01  0.01  0.01 -0.01  0.00  0.01 -0.02  0.01  0.01  0.01
O5         0.00  0.02  0.01  0.00  0.01  0.02  0.01  0.01 -0.01  0.01 -0.01
gender     0.02 -0.01 -0.03 -0.01  0.01  0.00  0.01  0.02  0.00  0.01 -0.02
education  0.00  0.00 -0.01  0.00  0.00 -0.01 -0.01  0.00 -0.01 -0.01  0.01
age        0.00  0.02  0.00  0.02 -0.01 -0.01  0.00 -0.01  0.00  0.00  0.00
             O3    O4    O5 gender education   age
A1         0.00  0.01  0.01   0.01      0.00 -0.02
A2         0.02  0.03 -0.01  -0.03     -0.01  0.02
A3         0.01  0.01 -0.01  -0.02     -0.01  0.03
A4         0.03  0.02 -0.01   0.00      0.00  0.03
A5         0.02  0.01 -0.01  -0.01      0.00  0.03
C1         0.00  0.03  0.01   0.01     -0.01  0.00
C2         0.01  0.03  0.00   0.01     -0.01  0.02
C3         0.01  0.02 -0.01   0.01     -0.01  0.02
C4        -0.01 -0.02  0.01  -0.01      0.00 -0.03
C5        -0.01  0.00  0.01   0.00     -0.01 -0.01
E1         0.00 -0.01  0.01   0.02      0.00  0.01
E2         0.02  0.00  0.00   0.02      0.00  0.00
E3        -0.02  0.01  0.02  -0.01      0.00  0.02
E4         0.00  0.01  0.01  -0.03     -0.01  0.00
E5         0.00  0.01  0.00  -0.01      0.00  0.02
N1        -0.02 -0.01  0.01   0.01      0.00 -0.01
N2        -0.01  0.00  0.02   0.00     -0.01 -0.01
N3         0.00  0.01  0.01   0.01     -0.01  0.00
N4         0.00 -0.02  0.01   0.02      0.00 -0.01
N5         0.01  0.01 -0.01   0.00     -0.01  0.00
O1         0.00  0.01  0.01   0.01     -0.01  0.00
O2         0.03  0.01 -0.01  -0.02      0.01  0.00
O3         0.00  0.02  0.01   0.01      0.00  0.01
O4         0.02  0.00  0.00   0.03     -0.01  0.01
O5         0.01  0.00  0.00  -0.01      0.00 -0.02
gender     0.01  0.03 -0.01   0.00      0.00  0.00
education  0.00 -0.01  0.00   0.00      0.00 -0.01
age        0.01  0.01 -0.02   0.00     -0.01  0.00

Types of missingness

Ideally our missingness is missing completely at random (MCAR). This means the probability of being missing is the same for all observations. If this is the case, our correlation estimates will be unbiased (if underpowered) and we’re free to use them with no concerns (other than the usual).

Aliens beam into a warehouse and randomly take some files.

Types of missingness

However, our data might be missing at random (MAR). This means the probability of being missing is different between cases, and also the probability is related to variables we have observed. This is not great, but sometimes we can account for this using the variables we have observed (e.g., imputation, different estimation methods).

Raccoons sneak into the warehouse and eat all the files by the door.

Types of missingness

It’s a problem if our data is missing not at random (MNAR). The probability of being missing differs for reasons that are unknown to us. This is especially problematic if the reason is associated with the variables at the heart of our study. Sensitivity analyses might help us detect MNAR-ness and possibly define the limits of our study, but we can’t adjust our data for this issue.

Criminals break into the warehouse and steal files about themselves.

Visualizing correlation matrices

A single correlation can be informative; a correlation matrix is more than the sum of its parts.

Correlation matrices can be used to infer larger patterns of relationships. You may be one of the gifted who can look at a matrix of numbers and see those patterns immediately. Or you can use heat maps to visualize correlation matrices.

library(corrplot)

corrplot(cor(bfi, use = "pairwise"), method = "square")

Beck, Condon, & Jackson, 2019

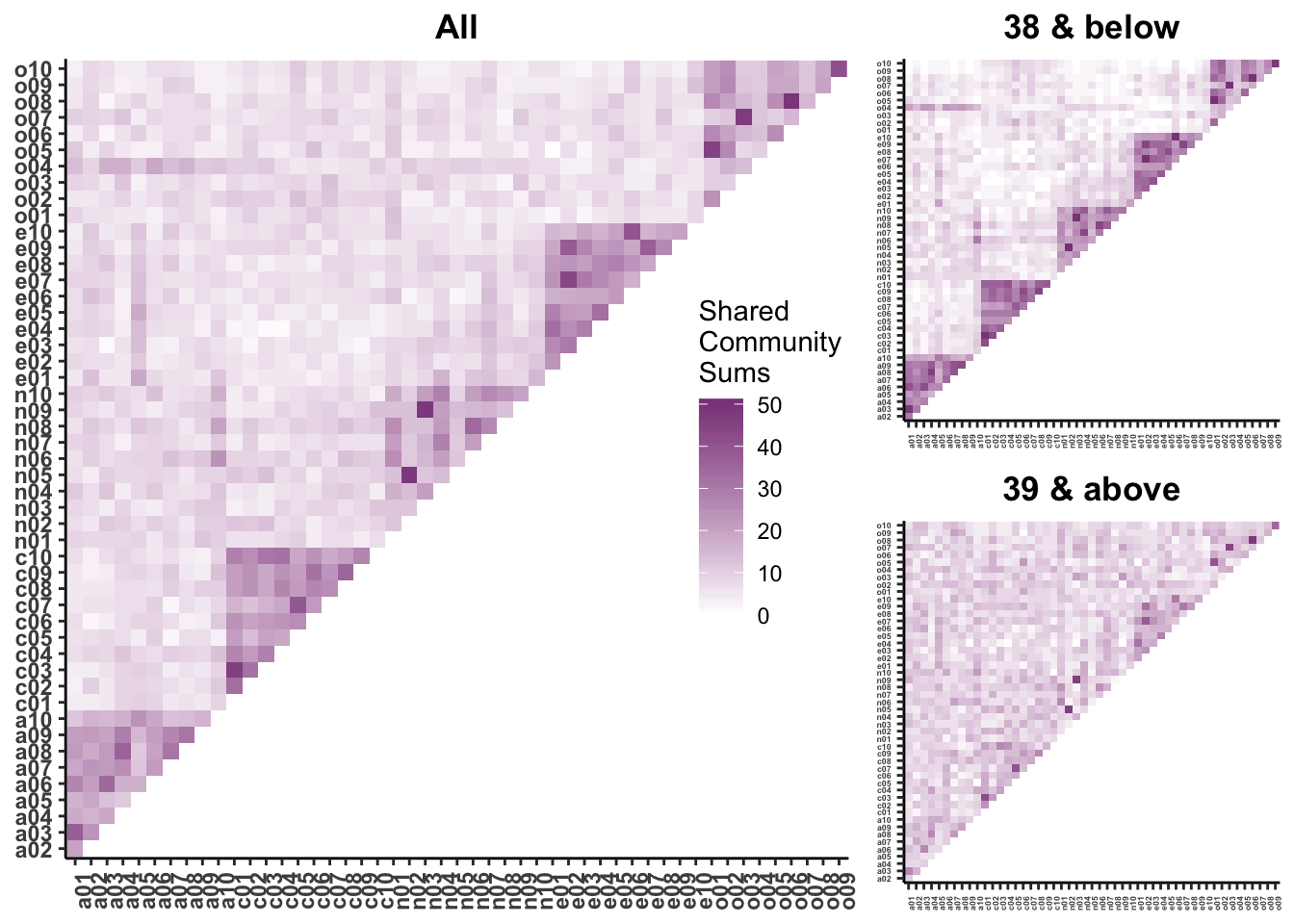
Factors that influence \(r\) (and most other test statistics)

Restriction of range (GRE scores and success)
Very skewed distributions (smoking and health)
Non-linear associations
Measurement overlap (modality and content)
Reliability

Reliability

Which would you rather have?

1-item final exam versus 30-item?
assessment via trained clinician vs tarot cards?
fMRI during minor earthquake vs no earthquake?

All measurement includes error

Score = true score + measurement error (CTT version)
Reliability assesses the consistency of measurement; high reliability indicates less error

Reliability

Cannot correlate error (randomness) with something
Because we do not measure our variables perfectly we get lower correlations compared to true correlations
If we want to have a valid measure it better be a reliable measure

Reliability

Think of reliability as a correlation with a measure and itself in a different world, at a different time, or a different but equal version

\[r_{XX}\]

Reliability

Reliability can be expressed as the proportion of true score variance over observed variance

How do you assess theoretical variance i.e., true score variance?

\[r_{XY} = r_{X_{T} Y_{T}} {\sqrt{r_{XX}r_{YY}}}\]

\[r_{XY} = .6 {\sqrt {(.70) (.70)}}\]

Reliability

\[r_{X_{T} Y_{T}} = = {\frac {r_{XY}} {\sqrt{r_{XX}r_{YY}}}}\] \[r_{X_{T} Y_{T}} = = {\frac {.30} {\sqrt{(.70)(.70)}}} = .42\]

Most common ways to assess

Cronbach’s alpha

library(psych)
alpha(dataset[,items])
alpha(bfi[,c("A1", "A2", "A3", "A4", "A5")])
## Gives average split half correlation
## Can tell you if you are assessing a single construct
## Conflicts with tidyverse - fix with psych::alpha()

Rest-retest reliability
Kappa or ICC

Reliability

if you are going to measure something, do it well
applies to ALL IVs and DVs, and all designs
remember this when interpreting research

Types of correlations

Many ways to get at relationship between two variables
Statistically the different types are almost exactly the same
Exist for historical reasons

Types of correlations

Point Biserial
- continuous and dichotomous
Phi coefficient
- both dichotomous
Spearman rank order
- ranked data
Biserial (assumes dichotomous is continuous)

Some important exceptions to the equivalence rule

Tetrachoric
- used for 2x2 contingency table
Polychoric
- ordinal variables
- extension of tetrachoric

Statistics and eugenics

The concept of the correlation is primarily attributed to Sir Frances Galton.

He was also the founder of the concept of eugenics.

The correlation coefficient was developed by his student, Karl Pearson, and adapted into the ANOVA framework by Sir Ronald Fisher.

Both were prominent advocates for the eugenics movement.

What do we do with this information?

Never use the correlation or the later techniques developed on it? Of course not.
Acknowledge this history? Certainly.
Understand how the perspectives of Galton, Fisher, Pearson and others shaped our practices? We must! – these are not set in stone, nor are they necessarily the best way to move forward.

Statistical significance was a way to avoid talking about nuance or degree.
“Correlation does not imply causation” was a refutation of work demonstrating associations between environment and poverty.

Next time….

Univariate regression