Interactions (Power analyses and 3-way interactions)

# Interactions (Power analyses and 3-way interactions)

---

## Power

The likelihood of finding an effect *if the effect actually exists.* Power gets larger as we:
* increase our sample size
* reduce (error) variance
* raise our Type I error rate
* study larger effects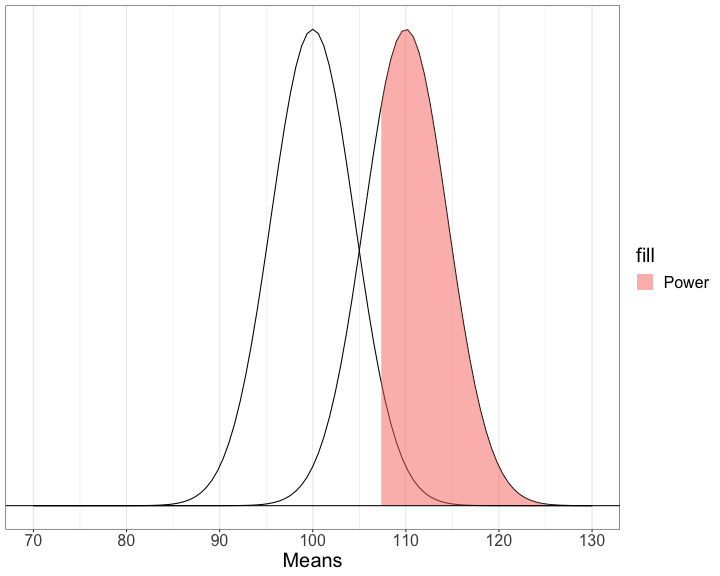

---

![](19-power_3way_files/figure-html/unnamed-chunk-2-1.png)

---

## Power in multiple regression (additive effects)

When calculating power for the omnibus test, use the expected multiple `$R^2$` value to calculate an effect size:

`$$\large f^2 = \frac{R^2}{1-R^2}$$`
---

### Omnibus power

```r
R2 = .10
(f = R2/(1-R2))
```

```
## [1] 0.1111111
```

```r
library(pwr)
pwr.f2.test(u = 3, # number of predictors in the model
            f2 = f, 
            sig.level = .05, #alpha
            power =.90) # desired power
```

```
## 
##      Multiple regression power calculation 
## 
##               u = 3
##               v = 127.5235
##              f2 = 0.1111111
##       sig.level = 0.05
##           power = 0.9
```

`v` is the denominator df of freedom, so the number of participants needed is v + p + 1.

---

### Coefficient power

To estimate power for a single coefficient, you need to consider (1) how much variance is accounted for by just the variable and (2) how much variance you'll account for in Y overall.

`$$\large f^2 = \frac{R^2_Y-R^2_{Y.X}}{1-R_Y^2}$$`
---
### Coefficient power

```r
R2 = .10
RX1 = .03
(f = (R2-RX1)/(1-R2))
```

```
## [1] 0.07777778
```

```r
pwr.f2.test(u = 3, # number of predictors in the model
            f2 = f, 
            sig.level = .05, #alpha
            power =.90) # desired power
```

```
## 
##      Multiple regression power calculation 
## 
##               u = 3
##               v = 182.1634
##              f2 = 0.07777778
##       sig.level = 0.05
##           power = 0.9
```

`v` is the denominator df of freedom, so the number of participants needed is v + p + 1.
---

## Effect sizes (interactions)

To start our discussion on powering interaction terms, we need to first consider the effect size of an interaction.

How big can we reasonably expect an interaction to be?

- Interactions are always partialled effects; that is, we examine the relationship between the product of variables X and Z only after we have controlled for X and controlled for Z. How does this affect the size of the relationship between XZ and Y?

???

The effect of XZ and Y will be made smaller as X or Z (or both) is related to the product -- the semi-partial correlation is always smaller than or equal to the zero-order correlation.

---

## McClelland and Judd (1993)

Is it more difficult to find interaction effects in experimental studies or observational studies?

What factors make it relatively easier to find interactions in experimental work?

---

### Factors influencing power in experimental studies

- No measurement error of IV 
    * don't have to guess what condition a participant is in
    * measurement error is exacerbated when two variables measured with error are multiplied by each other
    
- Studies with experimental designs are more likely to yield cross-over interactions; observational studies may be restricted to fan interactions
    * cross-over interactions are easier to detect than fan interactions
    
---

### Factors influencing power in experimental studies

- Researchers can concentrate scores on extreme ends on both X and Z.
    * increases variability in both X and Z, and in XZ
    * in observational studies, data tends to cluster around the mean

- Researchers can also force orthogonality in X and Z.

- Researchers can study the full range of X in an experiment.

---

### McClelland and Judd's simulation

For the experiment simulations, we used 2 X 2 factorial designs, with values of X and Z equal to +1 and —1 and an equal number of observations at each of the four combinations of X and Z values.

```r
X = rep(c(-1,1), each = 50)
Z = rep(c(-1,1), times = 50)
table(X,Z)
```

```
##     Z
## X    -1  1
##   -1 25 25
##   1  25 25
```

---

### McClelland and Judd's simulation

For the field study simulations, we used values of X and Z that varied between the extreme values of +1 and —1. ...values of X and Z were each sampled independently from a normal distribution with a mean of 0 and a standard deviation of 0.5. Values of X and Z were rounded to create equally spaced 9-point scales ranging from -1 to +1.

```r
score = function(x){
  new = 2*(x - min(x))/(max(x)-min(x))
  new_round = (round(new/.25)*.25)-1
  return(new_round)
}
X = rnorm(n = 100, mean = 0, sd = .5) %>% score()
Z = rnorm(n = 100, mean = 0, sd = .5) %>% score()

psych::describe(data.frame(X,Z), fast = T)
```

```
##   vars   n mean   sd min max range   se
## X    1 100 0.04 0.37  -1   1     2 0.04
## Z    2 100 0.01 0.48  -1   1     2 0.05
```
---

For the simulations of both the field studies and the experiments, `$\beta_0 = 0, \beta_X=\beta_Z=\beta_{XZ} = 1.$` There were 100 observations, and errors for the model were sampled from the same normal distribution with a mean of 0 and a standard deviation of 4.

```r
Y = 0 + 1*X + 1*Z + 1*X*Z + rnorm(n = 100, mean = 0, sd = 4)
summary(lm(Y ~ X*Z))
```

```
## 
## Call:
## lm(formula = Y ~ X * Z)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -6.4981 -2.2270 -0.0935  2.1595  7.6209 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)   0.2826     0.3322   0.851    0.397
## X            -0.5394     0.8952  -0.603    0.548
## Z            -0.4369     0.7019  -0.622    0.535
## X:Z           0.7171     1.9546   0.367    0.715
## 
## Residual standard error: 3.293 on 96 degrees of freedom
## Multiple R-squared:  0.008042,	Adjusted R-squared:  -0.02296 
## F-statistic: 0.2594 on 3 and 96 DF,  p-value: 0.8544
```

---

From 100 simulations each, estimates of the model parameter `$\beta_{XZ}$` the moderator or interaction effect equaled 0.977 and 0.979 for the field studies and experiments, respectively.

```r
set.seed(0309)
```

```r
# for experimental studies
sim = 100
ebeta_xz = numeric(length = 100)
et_xz = numeric(length = 100)
for(i in 1:sim){
  # simulate data
  X = rep(c(-1,1), each = 50)
  Z = rep(c(-1,1), times = 50)
 
  
   Y = 0 + 1*X + 1*Z + 1*X*Z + 
    rnorm(n = 100, mean = 0, sd = 4)
  #run model
  model = lm(Y ~ X*Z)
  coef = coef(summary(model))
  #extract coefficients
  beta = coef["X:Z", "Estimate"]
  t_val = coef["X:Z", "t value"]
  #save to vectors
  ebeta_xz[i] = beta
  et_xz[i] = t_val
}
```
]

```r
# for observational studies

obeta_xz = numeric(length = 100)
ot_xz = numeric(length = 100)
for(i in 1:sim){
  # simulate data
  X = rnorm(n = 100, mean = 0, sd = .5) %>% score()
  Z = rnorm(n = 100, mean = 0, sd = .5) %>% score()
  Y = 0 + 1*X + 1*Z + 1*X*Z + 
    rnorm(n = 100, mean = 0, sd = 4)
  #run model
  model = lm(Y ~ X*Z)
  coef = coef(summary(model))
  #extract coefficients
  beta = coef["X:Z", "Estimate"]
  t_val = coef["X:Z", "t value"]
  #save to vectors
  obeta_xz[i] = beta
  ot_xz[i] = t_val
}
```

]
---

```r
mean(ebeta_xz)
```

```
## [1] 1.018779
```

```r
mean(obeta_xz)
```

```
## [1] 0.6669377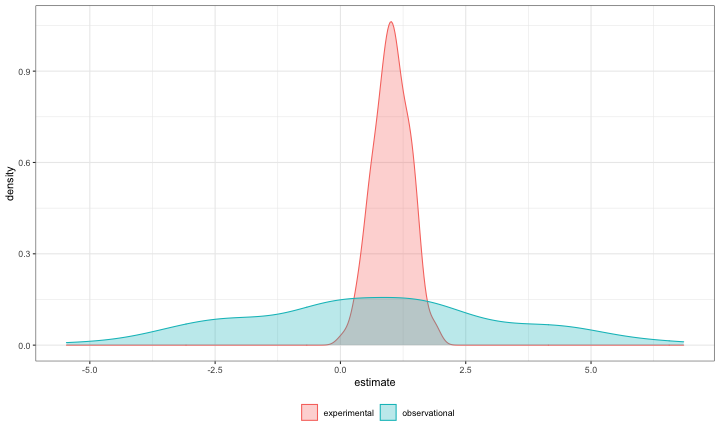
```

![](19-power_3way_files/figure-html/unnamed-chunk-12-1.png)

---

```r
mean(et_xz)
```

```
## [1] 2.568158
```

```r
mean(ot_xz)
```

```
## [1] 0.2903226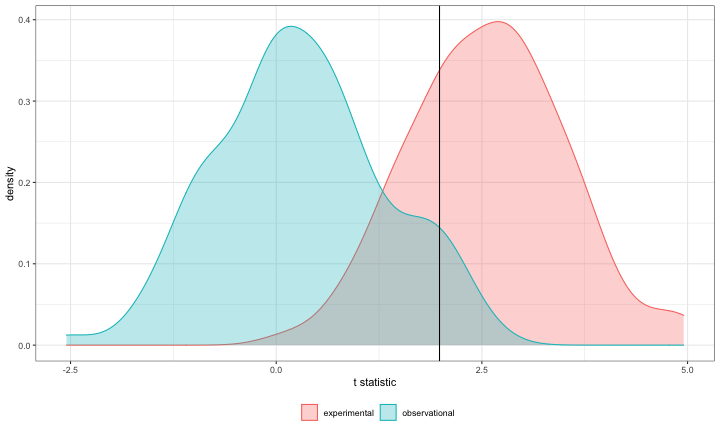
```

![](19-power_3way_files/figure-html/unnamed-chunk-14-1.png)

---

```r
cv = qt(p = .975, df = 100-3-1)
esig = et_xz > cv
sum(esig)
```

```
## [1] 72
```

```r
osig = ot_xz > cv
sum(osig)
```

```
## [1] 6
```

In our simulation, 72% of experimental studies were statistically significant, whereas only 6% of observational studies were significant. Remember, we built our simulation based on data where there really is an interaction effect (i.e., the null is false).

McClelland and Judd found that 74% of experimental studies and 9% of observational studies were significant.

---

### Efficiency

???
Efficiency = the ratio of the variance of XZ (controlling for X and Z) of a design to the best possible design (upper right corner). High efficiency is better; best efficiency is 1.

---

### Efficiency

.pull-left[
If the optimal design has N obserations, then to have the same standard error (i.e., the same power), any other design needs to have N*(1/efficency).

So a design with .06 efficency needs `$\frac{1}{.06} = 16.67$` times the sample size to detect the effect.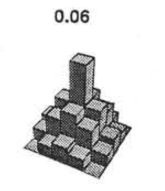 
]

This particular point has been ["rediscovered"](https://statmodeling.stat.columbia.edu/2018/03/15/need-16-times-sample-size-estimate-interaction-estimate-main-effect/) as recently as 2018:

* you need 16 times the sample size to detect an interaction as you need for a main effect of the same size.

???

This generalizes to higher-order interactions as well. If you have a three-way interaction, you need 16*16 (256 times the number of people).

---

## Observational studies: What NOT to do

Recode X and Z into more extreme values (e.g., median splits).

* While this increases variance in X and Z, it also increases measurement error.

Collect a random sample and then only perform analyses on the subsample with extreme values

* Reduces sample size and also generalizability.
    
#### What can be done?
M&J suggest oversampling extremes and using weighted and unweighted samples.

---

## Experimental studies: What NOT to do

Forget about lack of external validity and generalizability.

Ignore power when comparing interaction between covariate and experimental predictors (ANCOVA or multiple regression with categorical and continuous predictors).

---

## Three-way interactions and beyond

---

### Three-way interactions (regression)

**Regression equation**

`$$\hat{Y} = b_{0} + b_{1}X + b_{2}Z + b_{3}W + b_{4}XZ + b_{5}XW + b_{6}ZW + b_{7}XZW$$`
The three-way interaction qualifies the three main effects (and any two-way interactions).

Like a two-way interaction, the three-way interaction is a conditional effect.  And it is symmetrical, meaning there are several equally correct ways of interpreting it.

**Factorial ANOVA**

We describe the factorial ANOVA design by the number of levels of each factor. "X by Z by W" (e.g., 2 by 3 by 4, or 2x3x4)
---
A two-way  (A x B) interaction means that the magnitude of one main effect (e.g., A main effect) depends on levels of the other variable (B).  But, it is equally correct to say that the magnitude of the B main effect depends on levels of A. In regression, we refer to these as **conditional effects** and in ANOVA, they are called **simple main effects.**

A three-way interaction means that the magnitude of one two-way interaction (e.g., A x B) depends on levels of the remaining variable (C).

It is equally correct to say that the magnitude of the A x C interaction depend on levels of B. Or, that the magnitude of the B x C interaction depends on levels of A. These are known as **simple interaction effects**.

---
### Example (regression)

```r
#stress_data = read.csv()
# necessary for simple_slopes() function later
stress_data$gender = as.factor(stress_data$gender)

#always check your data!
psych::describe(stress_data, fast = T)
```

```
## Warning in FUN(newX[, i], ...): no non-missing arguments to min; returning Inf
```

```
## Warning in FUN(newX[, i], ...): no non-missing arguments to max; returning -Inf
```

```
##         vars   n  mean    sd min  max range   se
## gender     1 150   NaN    NA Inf -Inf  -Inf   NA
## bad_day    2 150  2.95  1.29   1    5     4 0.11
## talk       3 150  2.57  1.20   1    5     4 0.10
## stress     4 150 30.15 10.00   1   51    50 0.82
```

```r
table(stress_data$gender)
```

```
## 
## female   male 
##     67     83
```

---

```r
mod_stress = lm(stress ~ bad_day*talk*gender, data = stress_data)
summary(mod_stress)
```

```
## 
## Call:
## lm(formula = stress ~ bad_day * talk * gender, data = stress_data)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -10.6126  -3.2974   0.0671   3.1129  10.7774 
## 
## Coefficients:
##                         Estimate Std. Error t value  Pr(>|t|)    
## (Intercept)              20.3385     4.5181   4.502 0.0000139 ***
## bad_day                   2.5273     1.6596   1.523   0.13003    
## talk                      2.4870     1.3234   1.879   0.06227 .  
## gendermale               -0.1035     5.7548  -0.018   0.98568    
## bad_day:talk             -1.4220     0.4564  -3.116   0.00222 ** 
## bad_day:gendermale       -0.1244     2.0069  -0.062   0.95067    
## talk:gendermale           1.9797     2.2823   0.867   0.38718    
## bad_day:talk:gendermale   1.5260     0.7336   2.080   0.03931 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.733 on 142 degrees of freedom
## Multiple R-squared:  0.7865,	Adjusted R-squared:  0.776 
## F-statistic: 74.72 on 7 and 142 DF,  p-value: < 0.00000000000000022
```

---

```r
library(sjPlot)
plot_model(mod_stress, type = "pred", 
           terms = c("bad_day", # x-axis
                     "talk[meansd]", # color of lines
                     "gender")) # facets
```

![](19-power_3way_files/figure-html/unnamed-chunk-20-1.png)

---

```r
library(reghelper)
simple_slopes(mod_stress)
```

```
##     bad_day     talk gender Test Estimate Std. Error t value  df
## 1  1.661455 1.365903 sstest        5.8571     1.7437  3.3590 142
## 2  2.953333 1.365903 sstest        8.3892     1.5671  5.3535 142
## 3  4.245211 1.365903 sstest       10.9214     2.5606  4.2651 142
## 4  1.661455 2.566667 sstest       11.2788     1.4571  7.7406 142
## 5  2.953333 2.566667 sstest       16.1781     1.0985 14.7274 142
## 6  4.245211 2.566667 sstest       21.0775     1.6775 12.5647 142
## 7  1.661455 3.767431 sstest       16.7004     2.3888  6.9912 142
## 8  2.953333 3.767431 sstest       23.9670     1.4830 16.1608 142
## 9  4.245211 3.767431 sstest       31.2335     2.0578 15.1784 142
## 10 1.661455   sstest female        0.1245     0.7221  0.1724 142
## 11 2.953333   sstest female       -1.7125     0.5996 -2.8558 142
## 12 4.245211   sstest female       -3.5495     0.9450 -3.7561 142
## 13   sstest 1.365903 female        0.5850     1.0725  0.5455 142
## 14   sstest 2.566667 female       -1.1224     0.6181 -1.8160 142
## 15   sstest 3.767431 female       -2.8299     0.4630 -6.1115 142
## 16 1.661455   sstest   male        4.6396     1.0195  4.5510 142
## 17 2.953333   sstest   male        4.7741     0.6463  7.3862 142
## 18 4.245211   sstest   male        4.9085     0.9474  5.1813 142
## 19   sstest 1.365903   male        2.5451     0.5036  5.0533 142
## 20   sstest 2.566667   male        2.6700     0.6116  4.3655 142
## 21   sstest 3.767431   male        2.7950     1.2025  2.3244 142
##                 Pr(>|t|) Sig.
## 1              0.0010045   **
## 2      0.000000338609249  ***
## 3      0.000036272213402  ***
## 4      0.000000000001687  ***
## 5  < 0.00000000000000022  ***
## 6  < 0.00000000000000022  ***
## 7      0.000000000098063  ***
## 8  < 0.00000000000000022  ***
## 9  < 0.00000000000000022  ***
## 10             0.8633621     
## 11             0.0049366   **
## 12             0.0002511  ***
## 13             0.5862803     
## 14             0.0714796    .
## 15     0.000000009006053  ***
## 16     0.000011367217054  ***
## 17     0.000000000011768  ***
## 18     0.000000741793346  ***
## 19     0.000001314710277  ***
## 20     0.000024272959555  ***
## 21             0.0215233    *
```

---

```r
# choose levels of the moderator to test
mylist = list(gender = c("male", "female"),
              talk = c(1.4, 2.6, 3.8))
simple_slopes(mod_stress, levels = mylist)
```

```
##   bad_day talk gender Test Estimate Std. Error t value  df       Pr(>|t|) Sig.
## 1  sstest  1.4   male        2.5486     0.4939  5.1601 142 0.000000816169  ***
## 2  sstest  2.6   male        2.6735     0.6253  4.2756 142 0.000034791467  ***
## 3  sstest  3.8   male        2.7983     1.2199  2.2939 142        0.02327    *
## 4  sstest  1.4 female        0.5365     1.0584  0.5069 142        0.61298     
## 5  sstest  2.6 female       -1.1698     0.6077 -1.9251 142        0.05622    .
## 6  sstest  3.8 female       -2.8762     0.4671 -6.1569 142 0.000000007187  ***
```

---

As a reminder, centering will change all but the highest-order terms in a model.

```r
stress_c = stress_data %>%
  mutate(
    across( c(bad_day, talk) , ~.x-mean(.x) )
    )

mod_c = lm(stress ~ bad_day*talk*gender, data = stress_c)
```

---

```r
library(broom)
tidy(mod_stress)
```

```
## # A tibble: 8 x 5
##   term                    estimate std.error statistic   p.value
##   <chr>                      <dbl>     <dbl>     <dbl>     <dbl>
## 1 (Intercept)               20.3       4.52     4.50   0.0000139
## 2 bad_day                    2.53      1.66     1.52   0.130    
## 3 talk                       2.49      1.32     1.88   0.0623   
## 4 gendermale                -0.104     5.75    -0.0180 0.986    
## 5 bad_day:talk              -1.42      0.456   -3.12   0.00222  
## 6 bad_day:gendermale        -0.124     2.01    -0.0620 0.951    
## 7 talk:gendermale            1.98      2.28     0.867  0.387    
## 8 bad_day:talk:gendermale    1.53      0.734    2.08   0.0393
```

```r
tidy(mod_c)
```

```
## # A tibble: 8 x 5
##   term                    estimate std.error statistic  p.value
##   <chr>                      <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)                23.4      0.845     27.7  3.89e-59
## 2 bad_day                    -1.12     0.618     -1.82 7.15e- 2
## 3 talk                       -1.71     0.600     -2.86 4.94e- 3
## 4 gendermale                 16.2      1.10      14.7  2.20e-30
## 5 bad_day:talk               -1.42     0.456     -3.12 2.22e- 3
## 6 bad_day:gendermale          3.79     0.870      4.36 2.47e- 5
## 7 talk:gendermale             6.49     0.882      7.36 1.38e-11
## 8 bad_day:talk:gendermale     1.53     0.734      2.08 3.93e- 2
```

---
### Four-way?

$$
`\begin{aligned}
\hat{Y} &= b_0 + b_1X + b_{2}Z + b_{3}W + b_{4}Q + b_{5}XW\\
&+ b_{6}ZW + b_{7}XZ + b_{8}QX + b_{9}QZ + b_{10}QW\\
&+ b_{11}XZQ + b_{12}XZW + b_{13}XWQ + b_{14}ZWQ + b_{15}XZWQ\\
\end{aligned}`
$$

3-way (and higher) interactions are incredibly difficult to interpret, in part because they represent incredibly complicated processes. If you have a solid theoretical rationale for conducting a 3-day interaction, be sure you've collected enough subjects to power your test (more on this later).

---

Especially with small samples, three-way interactions may be the result of a few outliers skewing a regression line. If you have stumbled upon a three-way interaction during exploratory analyses, **be careful.** This is far more likely to be a result of over-fitting than uncovering a true underlying process.

Best practice for 3-way (and higher) interactions is to use at least one nominal moderator (ideally with only 2 levels), instead of all continuous moderators. This allows you to examine the 2-way interaction at each level of the nominal moderator.

Even better if one of these moderators is experimenter manipulated, which increases the likelihood of balanced conditions.

---

## Next time...

Polynomials and bootstrapping