Multiple Regression

class: center, middle, inverse, title-slide

# Multiple Regression

---

## Last time

- Semi-partial and partial correlations

## Today

- Introduction to multiple regression

---

## Regression equation

`$$\large \hat{Y} = b_0 + b_1X_1 + b_2X_2 + \dots+b_kX_k$$`

- regression coefficients are "partial" regression coefficients

- predicted change in `$Y$` for a 1 unit change in `$X$`, *holding all other predictors constant* 
  
  - similar to semi-partial correlation -- represents part of each `$X$`

---

## example

```r
library(here)
stress.data = read.csv(here("data/stress.csv")) %>% select(-group)
library(psych)
describe(stress.data, fast = T)
```

```
##         vars   n   mean     sd  min    max  range    se
## id         1 118 488.65 295.95 2.00 986.00 984.00 27.24
## Anxiety    2 118   7.61   2.49 0.70  14.64  13.94  0.23
## Stress     3 118   5.18   1.88 0.62  10.32   9.71  0.17
## Support    4 118   8.73   3.28 0.02  17.34  17.32  0.30
```

```r
round(cor(stress.data),2)
```

```
##            id Anxiety Stress Support
## id       1.00    0.07  -0.05   -0.03
## Anxiety  0.07    1.00  -0.05   -0.55
## Stress  -0.05   -0.05   1.00    0.52
## Support -0.03   -0.55   0.52    1.00
```

---

## example

```r
mr.model <- lm(Stress ~ Support + Anxiety, data = stress.data)
summary(mr.model)
```

```
...
## Coefficients:
##             Estimate Std. Error t value         Pr(>|t|)    
## (Intercept) -0.31587    0.85596  -0.369         0.712792    
## Support      0.40618    0.05115   7.941 0.00000000000149 ***
## Anxiety      0.25609    0.06740   3.799         0.000234 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.519 on 115 degrees of freedom
## Multiple R-squared:  0.3556,	Adjusted R-squared:  0.3444 
## F-statistic: 31.73 on 2 and 115 DF,  p-value: 0.00000000001062
...
```

???

If a univariate regression is estimating the best-fit line, what is this estimating?

---
## Visualizing multiple regression

```r
library(visreg)

visreg2d(mr.model,"Support", "Anxiety", plot.type = "persp")
```

![](8-m_regression_files/figure-html/unnamed-chunk-4-1.png)

---

## Calculating coefficients

Just like with univariate regression, we calculate the OLS solution. As a reminder, this calculation will yield the estimate that reduces the sum of the squared deviations from the line:

.pull-left[
### Unstandardized
`$$\large \hat{Y} = b_0 + b_{1}X1 + b_{2}X_2$$`
$$\large \text{minimize} \sum (Y-\hat{Y})^2 $$
]
.pull-right[

### Standardized
`$$\large \hat{Z}_{Y} = b_{1}^*Z_{X1} + b_{2}^*Z_{X2}$$`
`$$\large \text{minimize} \sum (z_{Y}-\hat{z}_{Y})^2$$`
]

---
## Calculating the standardized regression coefficient

`$$b_{1}^* = \frac{r_{Y1}-r_{Y2}r_{12}}{1-r_{12}^2}$$`

`$$b_{2}^* = \frac{r_{Y2}-r_{Y1}r_{12}}{1-r_{12}^2}$$`

---

## Relationships between partial, semi- and b*

(Standardized) Regression coefficients, partial correlations, and semi-partial correlations are all ways to represent the relationship between two variables while taking into account a third (or more!) variables.

- Each is a standardized effect, meaning the effect size is calculated in standardized units, bounded by -1 and 1*. This means they can be compared across studies, metrics, etc.

Note, however, that the calculations differ between the three effect sizes. These effect sizes are not synonymous and often yield different answers.

- if predictors are not correlated, `$r$`,  sr `$(r_{Y(1.2)})$` and b* are equal

.small[*Actually, standardized regression coefficients are not bounded by -1 and 1, but it's rare to see values this large, and [usually indicative of some multicollinearity](http://www.statmodel.com/download/Joreskog.pdf).]
---

** Standardized multiple regression coefficient** `$b^*$`

`$$\large \frac{r_{Y1}-r_{Y2}r_{12}}{1-r_{12}^2}$$`

** Semi-partial correlation** `$r_{y(1.2)}$`
`$$\large \frac{r_{Y1}-r_{Y2}r_{Y12} }{\sqrt{1-r_{12}^2}}$$`

** Partial correlation** `$r_{y1.2}$`
`$$\large \frac{r_{Y1}-r_{Y2}r_{{12}}}{\sqrt{1-r^2_{Y2}}\sqrt{1-r^2_{12}}}$$`

---

```r
stress.data = stress.data %>%
  mutate(z_anxiety = scale(Anxiety),
         z_support = scale(Support),
         z_stress = scale(Stress))

mod0 = lm(z_stress ~ z_anxiety + z_support, 
          data = stress.data)

round(coef(mod0),3)
```

```
## (Intercept)   z_anxiety   z_support 
##       0.000       0.339       0.710
```

.pull-left[

```r
spcor.test(x = stress.data$Stress, 
           y = stress.data$Anxiety, 
           z = stress.data$Support)$estimate
```

```
## [1] 0.2844005
```
]

.pull-right[

```r
pcor.test(x = stress.data$Stress, 
          y = stress.data$Anxiety, 
          z = stress.data$Support)$estimate
```

```
## [1] 0.3339479
```

]
---
    
## Original metric

`$$b_{1} = b_{1}^*\frac{s_{Y}}{s_{X1}}$$`

`$$b_{1}^* = b_{1}\frac{s_{X1}}{s_{Y}}$$`

### Intercept

`$$b_{0} = \bar{Y} - b_{1}\bar{X_{1}} - b_{2}\bar{X_{2}}$$`
---

```r
mr.model <- lm(Stress ~ Support + Anxiety, data = stress.data)
summary(mr.model)
```

```
## 
## Call:
## lm(formula = Stress ~ Support + Anxiety, data = stress.data)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.1958 -0.8994 -0.1370  0.9990  3.6995 
## 
## Coefficients:
##             Estimate Std. Error t value         Pr(>|t|)    
*## (Intercept) -0.31587    0.85596  -0.369         0.712792    
## Support      0.40618    0.05115   7.941 0.00000000000149 ***
## Anxiety      0.25609    0.06740   3.799         0.000234 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.519 on 115 degrees of freedom
## Multiple R-squared:  0.3556,	Adjusted R-squared:  0.3444 
## F-statistic: 31.73 on 2 and 115 DF,  p-value: 0.00000000001062
```

---

```r
mr.model <- lm(Stress ~ Support + Anxiety, data = stress.data)
summary(mr.model)
```

```
## 
## Call:
## lm(formula = Stress ~ Support + Anxiety, data = stress.data)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.1958 -0.8994 -0.1370  0.9990  3.6995 
## 
## Coefficients:
##             Estimate Std. Error t value         Pr(>|t|)    
## (Intercept) -0.31587    0.85596  -0.369         0.712792    
*## Support      0.40618    0.05115   7.941 0.00000000000149 ***
*## Anxiety      0.25609    0.06740   3.799         0.000234 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.519 on 115 degrees of freedom
## Multiple R-squared:  0.3556,	Adjusted R-squared:  0.3444 
## F-statistic: 31.73 on 2 and 115 DF,  p-value: 0.00000000001062
```

---

## "Controlling for"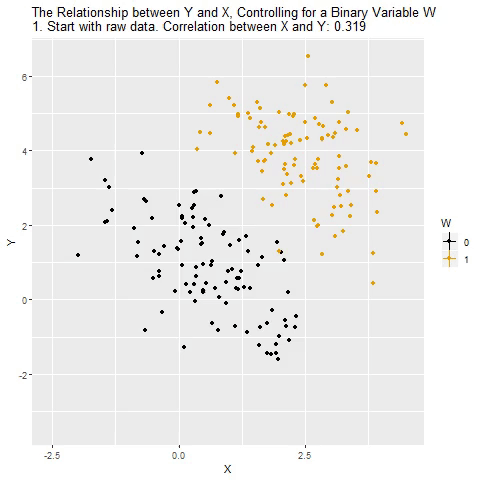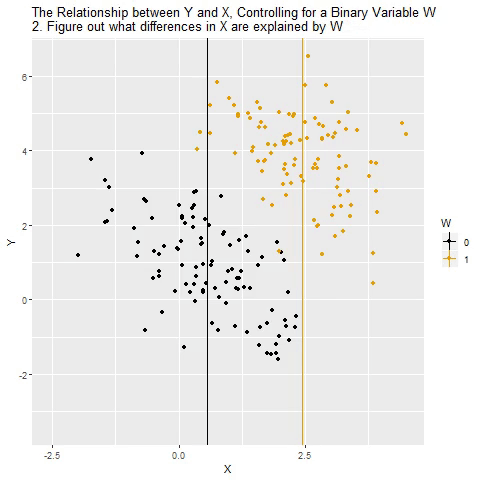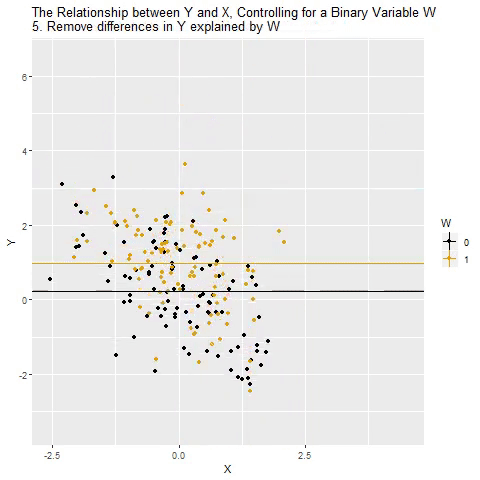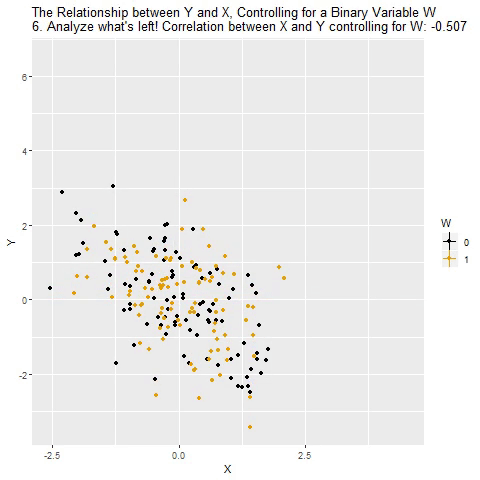

![](images/control.gif)

Taken from [@nickchk](https://twitter.com/nickchk)

---

## Matrix algebra

As we add variables to our model, the calculation of coefficient estimates using correlations and partial correlations gets more complicated. We'll only consider the formulas for the case of multiple regression with two variables, because as we move to three or more, these formulas become unreadable, although our interpretations are the same.

But the matrix algebra calculations for coefficients remain the same.

---

## Matrix algebra

.pull-left[

### Univariate regression

`$$(\mathbf{X'X})^{-1} \mathbf{X'y}=\mathbf{b}$$`
Where `$\mathbf{X}$` is an `$n \times 2$` matrix, where the first column is composed of 1's and the second column are participant's scores on X.
]

.pull-left[

### Mutiple regression

`$$(\mathbf{X'X})^{-1} \mathbf{X'y}=\mathbf{b}$$`

Where `$\mathbf{X}$` is an `$n \times (k+1)$` matrix, where the first column is composed of 1's and the columns 2-(k+1) are participant's scores on k IV's `$(X_1...X_{K})$`.
]

---

```r
X.mat = cbind(1,stress.data[,c("Anxiety", "Support")])
X.mat = as.matrix(X.mat)

y.mat = as.matrix(stress.data[,c("Stress")])

solve(t(X.mat) %*% X.mat) %*% t(X.mat) %*% y.mat
```

```
##               [,1]
## 1       -0.3158660
## Anxiety  0.2560870
## Support  0.4061785
```

```r
coef(mr.model)
```

```
## (Intercept)     Support     Anxiety 
##  -0.3158660   0.4061785   0.2560870
```

---

## Estimating model fit

```r
mr.model <- lm(Stress ~ Support + Anxiety, data = stress.data)
summary(mr.model)
```

```
## 
## Call:
## lm(formula = Stress ~ Support + Anxiety, data = stress.data)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.1958 -0.8994 -0.1370  0.9990  3.6995 
## 
## Coefficients:
##             Estimate Std. Error t value         Pr(>|t|)    
## (Intercept) -0.31587    0.85596  -0.369         0.712792    
## Support      0.40618    0.05115   7.941 0.00000000000149 ***
## Anxiety      0.25609    0.06740   3.799         0.000234 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.519 on 115 degrees of freedom
*## Multiple R-squared:  0.3556,	Adjusted R-squared:  0.3444 
## F-statistic: 31.73 on 2 and 115 DF,  p-value: 0.00000000001062
```

---

```r
library(broom); library(scales)
stress.data1 = augment(mr.model)
stress.data1 %>%
  ggplot(aes(x = Stress, y = .fitted)) + geom_point() + geom_hline(aes(yintercept = mean(Stress), color = "bar(Y)")) + geom_smooth(method = "lm", aes(color = "R[bar(Y)][Y]")) + scale_x_continuous("Y (Stress)") + scale_color_discrete(labels = parse_format()) + scale_y_continuous(expression(hat(Y))) + theme_bw(base_size = 20)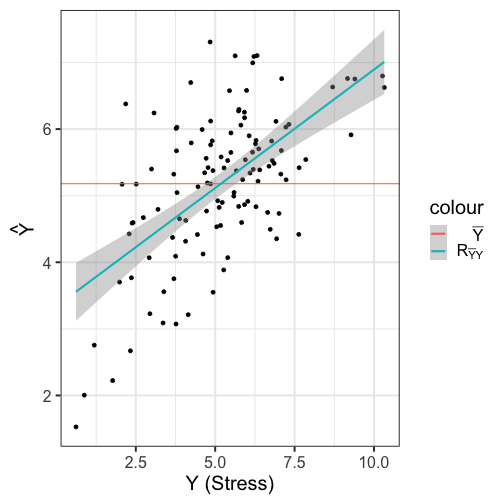
```

![](8-m_regression_files/figure-html/unnamed-chunk-12-1.png)

---
## Multiple correlation, R

`$$\large \hat{Y} = b_{0} + b_{1}X_{1} + b_{2}X_{2}$$`

- `$\hat{Y}$` is a linear combination of Xs
- `$r_{Y\hat{Y}}$` = multiple correlation = R

`$$\large R = \sqrt{b_{1}^*r_{Y1} + b_{2}^*r_{Y2}}$$`
`$$\large R^2 = {b_{1}^*r_{Y1} + b_{2}^*r_{Y2}}$$`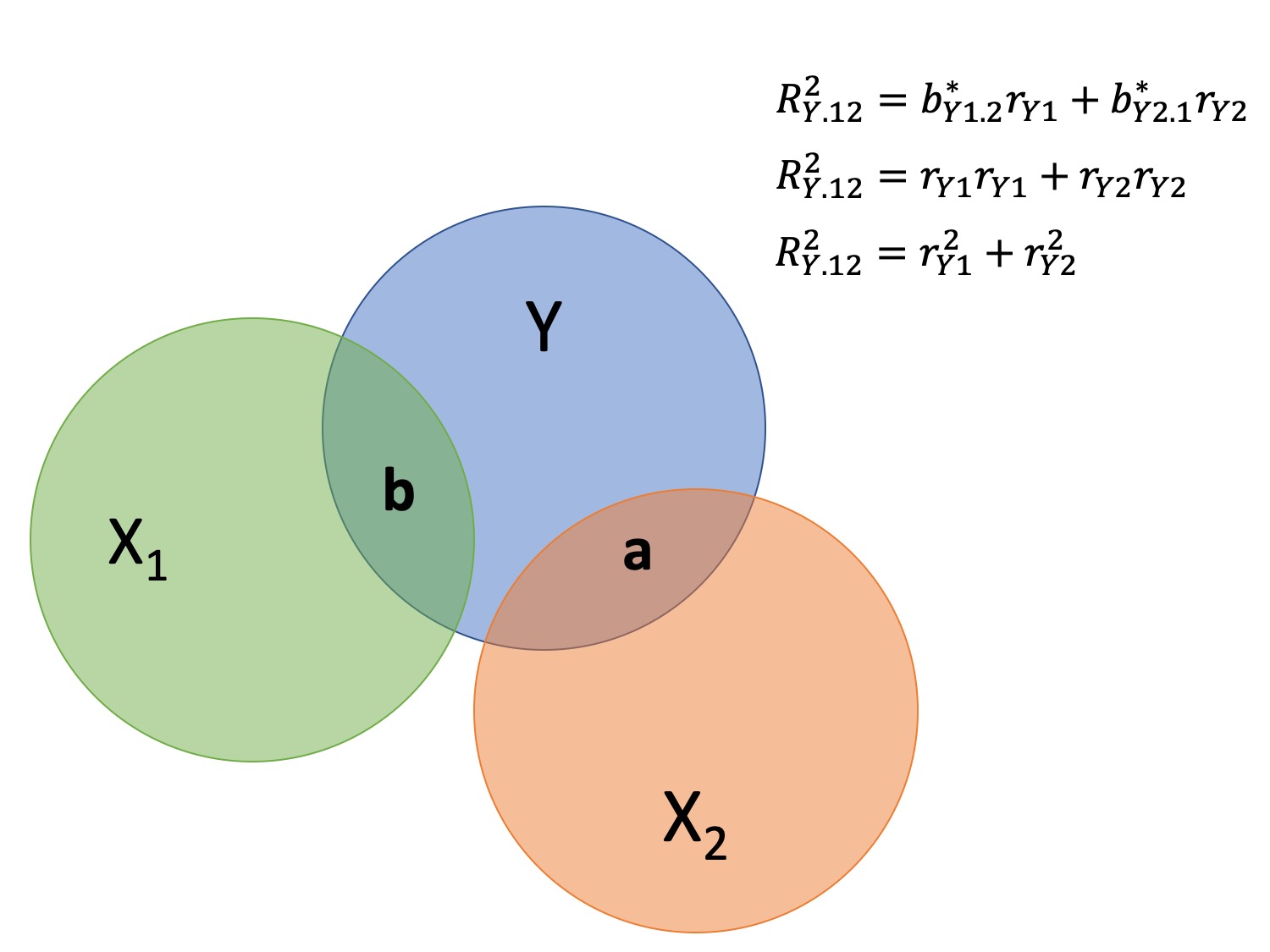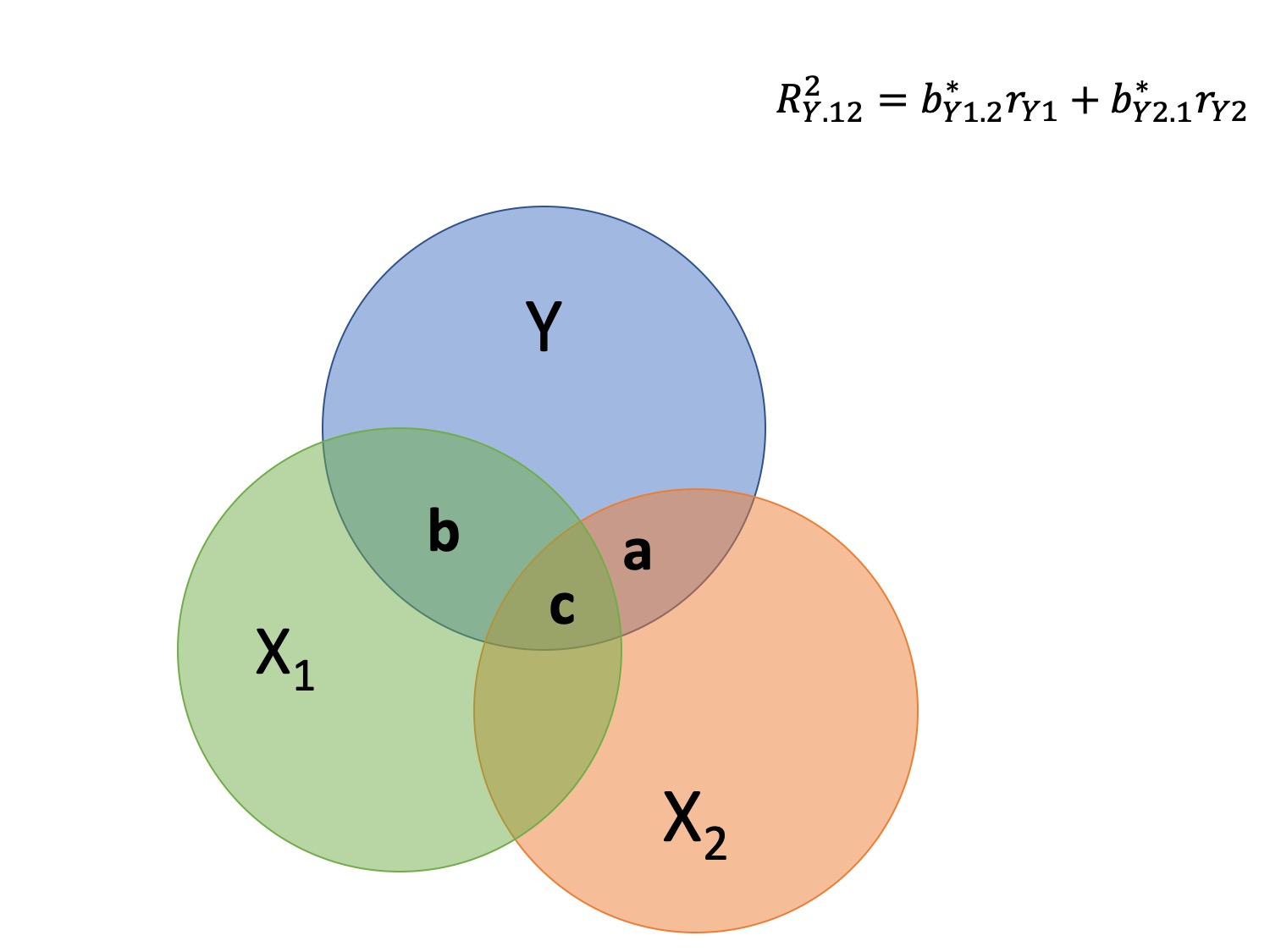

---

![](images/venn/Slide7.jpeg)
---

![](images/venn/Slide8.jpeg)

---
## Decomposing sums of squares

We haven't changed our method of decomposing variance from the univariate model

`$$\Large \frac{SS_{regression}}{SS_{Y}} = R^2$$`
`$$\Large {SS_{regression}} = R^2({SS_{Y})}$$`

`$$\Large {SS_{residual}} = (1- R^2){SS_{Y}}$$`
  
---

## significance tests

- `$R^2$` (omnibus)  
- Regression Coefficients  
- Increments to `$R^2$`  
    
---

## R-squared, `$R^2$`

- Same interpretation as before

- Adding predictors into your model will increase `$R^2$` – regardless of whether or not the predictor is significantly correlated with Y.

- Think back to sampling error. If the population correlation, `$\rho$`, is 0, will your sample estimate always be 0?

- Adjusted/Shrunken `$R^2$` takes into account the number of predictors in your model

---

## Adjusted R-squared, `$\text{Adj } R^2$`

`$$\large R_{A}^2 = 1 - (1 -R^2)\frac{n-1}{n-p-1}$$`

- What happens if you add many IV's to your model that are uncorrelated with your DV?

- What happens as you add more covariates to your model that are highly correlated with your key predictor, X?

`$$b_{1}^* = \frac{r_{Y1}-r_{Y2}r_{12}}{1-r_{12}^2}$$`

---

## ANOVA

```r
summary(mr.model)
```

```
## 
## Call:
## lm(formula = Stress ~ Support + Anxiety, data = stress.data)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.1958 -0.8994 -0.1370  0.9990  3.6995 
## 
## Coefficients:
##             Estimate Std. Error t value         Pr(>|t|)    
## (Intercept) -0.31587    0.85596  -0.369         0.712792    
## Support      0.40618    0.05115   7.941 0.00000000000149 ***
## Anxiety      0.25609    0.06740   3.799         0.000234 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.519 on 115 degrees of freedom
## Multiple R-squared:  0.3556,	Adjusted R-squared:  0.3444 
*## F-statistic: 31.73 on 2 and 115 DF,  p-value: 0.00000000001062
```
---

## ANOVA

The omnibus test uses all SS associated with predictors.

```r
anova(mr.model)
```

```
## Analysis of Variance Table
## 
## Response: Stress
##            Df  Sum Sq Mean Sq F value          Pr(>F)    
*## Support     1 113.151 113.151  49.028 0.0000000001807 ***
*## Anxiety     1  33.314  33.314  14.435       0.0002336 ***
## Residuals 115 265.407   2.308                            
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

Note that the _p_-values in this table do NOT match the _p_-values in the regression summary table. For the time being, just know that, in a multiple regression framework, you should use the `summary()` output to interpret the unique contribution of predictors, not the `anova()` output. We'll return to these calculations later in the term and discuss them in more detail. 
---

```r
summary(mr.model)
```

```
## 
## Call:
## lm(formula = Stress ~ Support + Anxiety, data = stress.data)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.1958 -0.8994 -0.1370  0.9990  3.6995 
## 
## Coefficients:
##             Estimate Std. Error t value         Pr(>|t|)    
## (Intercept) -0.31587    0.85596  -0.369         0.712792    
*## Support      0.40618    0.05115   7.941 0.00000000000149 ***
*## Anxiety      0.25609    0.06740   3.799         0.000234 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.519 on 115 degrees of freedom
## Multiple R-squared:  0.3556,	Adjusted R-squared:  0.3444 
## F-statistic: 31.73 on 2 and 115 DF,  p-value: 0.00000000001062
```

---

## Standard errors

`$$\Large H_{0}: \beta_{X}= 0$$`
`$$\Large H_{1}: \beta_{X} \neq 0$$`

---

## Standard error of regression coefficient

In the case of univariate regression:

`$$\Large se_{b} = \frac{s_{Y}}{s_{X}}{\sqrt{\frac {1-r_{xy}^2}{n-2}}}$$`

In the case of multiple regression:

`$$\Large se_{b} = \frac{s_{Y}}{s_{X}}{\sqrt{\frac {1-R_{Y\hat{Y}}^2}{n-p-1}}} \sqrt{\frac {1}{1-R_{i.jkl...p}^2}}$$`

- As N increases... 
- As variance explained increases...

---

`$$se_{b} = \frac{s_{Y}}{s_{X}}{\sqrt{\frac {1-R_{Y\hat{Y}}^2}{n-p-1}}} \sqrt{\frac {1}{1-R_{i.jkl...p}^2}}$$`

## Tolerance

`$$1-R_{i.jkl...p}^2$$`

- Proportion of `$X_i$` that does not overlap with other predictors.
    - Bounded by 0 and 1

- Large tolerance (little overlap) means standard error will be small.

- what does this mean for including a lot of variables in your model?

---

## Tolerance in `R`

```r
library(olsrr)

ols_vif_tol(mr.model)
```

```
##   Variables Tolerance      VIF
## 1   Support  0.701857 1.424792
## 2   Anxiety  0.701857 1.424792
```

Why are tolerance values identical here?

---

## Which variables to include

- You goal should be to match the population model (theoretically)

- Including many variables will not bias parameter estimates but will potentially increase degrees of freedom and standard errors; in other words, putting too many variables in your model may make it _more difficult_ to find a statistically significant result

- But that's only the case if you add variables unrelated to Y or X; there are some cases in which adding the wrong variables can lead to spurious results. [Stay tuned for the lecture on causal models.]

---

class: inverse

## Next time...

Model comparisons

Categorical predictors