class: center, middle, inverse, title-slide # Review and Machine Learning --- #Last time... * Polynomials * Bootstrapping # Today * Review * Lessons from machine learning --- ### Data Examples today are based on data from the [2015 World Happiness Report](https://worldhappiness.report/ed/2015/), which is an annual survey part of the [Gallup World Poll](https://www.gallup.com/178667/gallup-world-poll-work.aspx). ```r library(tidyverse) data = read.csv("https://raw.githubusercontent.com/uopsych/psy612/master/data/world_happiness_2015.csv") glimpse(data) ``` ``` ## Rows: 136 ## Columns: 10 ## $ Country <chr> "Albania", "Argentina", "Armenia", "Australia", "Austria", … ## $ Happiness <dbl> 4.606651, 6.697131, 4.348320, 7.309061, 7.076447, 5.146775,… ## $ GDP <dbl> 9.251464, NA, 8.968936, 10.680326, 10.691354, 9.730904, NA,… ## $ Support <dbl> 0.6393561, 0.9264923, 0.7225510, 0.9518616, 0.9281103, 0.78… ## $ Life <dbl> 68.43517, 67.28722, 65.30076, 72.56024, 70.82256, 61.97585,… ## $ Freedom <dbl> 0.7038507, 0.8812237, 0.5510266, 0.9218710, 0.9003052, 0.76… ## $ Generosity <dbl> -0.082337685, NA, -0.186696529, 0.315701962, 0.089088559, -… ## $ Corruption <dbl> 0.8847930, 0.8509062, 0.9014622, 0.3565544, 0.5574796, 0.61… ## $ World <int> 2, 4, 2, 1, 1, 2, 4, 3, 2, 1, 3, 3, 4, 2, 4, 4, 3, 3, 4, 1,… ## $ Hemisphere <chr> "East", "West", "East", "East", "East", "East", "East", "Ea… ``` --- ### Data ```r data = data %>% mutate( World_simple = case_when( World %in% c(1,2) ~ "1/2", World %in% c(3,4) ~ "3/4"), World = as.factor(World)) glimpse(data) ``` ``` ## Rows: 136 ## Columns: 11 ## $ Country <chr> "Albania", "Argentina", "Armenia", "Australia", "Austria"… ## $ Happiness <dbl> 4.606651, 6.697131, 4.348320, 7.309061, 7.076447, 5.14677… ## $ GDP <dbl> 9.251464, NA, 8.968936, 10.680326, 10.691354, 9.730904, N… ## $ Support <dbl> 0.6393561, 0.9264923, 0.7225510, 0.9518616, 0.9281103, 0.… ## $ Life <dbl> 68.43517, 67.28722, 65.30076, 72.56024, 70.82256, 61.9758… ## $ Freedom <dbl> 0.7038507, 0.8812237, 0.5510266, 0.9218710, 0.9003052, 0.… ## $ Generosity <dbl> -0.082337685, NA, -0.186696529, 0.315701962, 0.089088559,… ## $ Corruption <dbl> 0.8847930, 0.8509062, 0.9014622, 0.3565544, 0.5574796, 0.… ## $ World <fct> 2, 4, 2, 1, 1, 2, 4, 3, 2, 1, 3, 3, 4, 2, 4, 4, 3, 3, 4, … ## $ Hemisphere <chr> "East", "West", "East", "East", "East", "East", "East", "… ## $ World_simple <chr> "1/2", "3/4", "1/2", "1/2", "1/2", "1/2", "3/4", "3/4", "… ``` --- ## Concept 1: Interpreting the output of linear models. ```r mod1 = lm(Happiness ~ Life, data = data) mod2 = lm(Happiness ~ Life + GDP, data = data) mod3 = lm(Happiness ~ Life*GDP, data = data) mod4 = lm(Happiness ~ Life + World_simple, data = data) mod5 = lm(Happiness ~ Life*World_simple, data = data) library(sjPlot) tab_model(mod1, mod2, mod3, mod4, mod5, show.p = F, show.ci = F, p.style = "stars", dv.labels = paste0("mod", 1:5)) ``` --- <table style="border-collapse:collapse; border:none;"> <tr> <th style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; text-align:left; "> </th> <th colspan="1" style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; ">mod1</th> <th colspan="1" style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; ">mod2</th> <th colspan="1" style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; ">mod3</th> <th colspan="1" style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; ">mod4</th> <th colspan="1" style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; ">mod5</th> </tr> <tr> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; text-align:left; ">Predictors</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">Estimates</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">Estimates</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">Estimates</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">Estimates</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">Estimates</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">(Intercept)</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">-1.48 <sup>**</sup></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">-2.40 <sup>***</sup></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">8.65 <sup>*</sup></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">-1.22 <sup></sup></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">-3.55 <sup></sup></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">Life</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.11 <sup>***</sup></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.03 <sup>*</sup></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">-0.15 <sup>*</sup></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.11 <sup>***</sup></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.14 <sup>***</sup></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">GDP</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.61 <sup>***</sup></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">-0.64 <sup></sup></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">Life * GDP</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.02 <sup>**</sup></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">World_simple [3/4]</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">-0.10 <sup></sup></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">2.60 <sup></sup></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">Life * World_simple [3/4]</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">-0.04 <sup></sup></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm; border-top:1px solid;">Observations</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left; border-top:1px solid;" colspan="1">135</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left; border-top:1px solid;" colspan="1">121</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left; border-top:1px solid;" colspan="1">121</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left; border-top:1px solid;" colspan="1">135</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left; border-top:1px solid;" colspan="1">135</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm;">R<sup>2</sup> / R<sup>2</sup> adjusted</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="1">0.540 / 0.537</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="1">0.687 / 0.682</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="1">0.708 / 0.700</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="1">0.541 / 0.534</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="1">0.548 / 0.538</td> </tr> <tr> <td colspan="6" style="font-style:italic; border-top:double black; text-align:right;">* p<0.05 ** p<0.01 *** p<0.001</td> </tr> </table> --- ### One continuous predictor 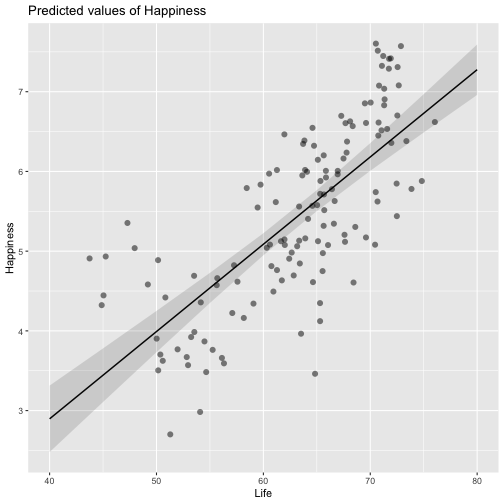<!-- --> --- ### Two continuous predictors 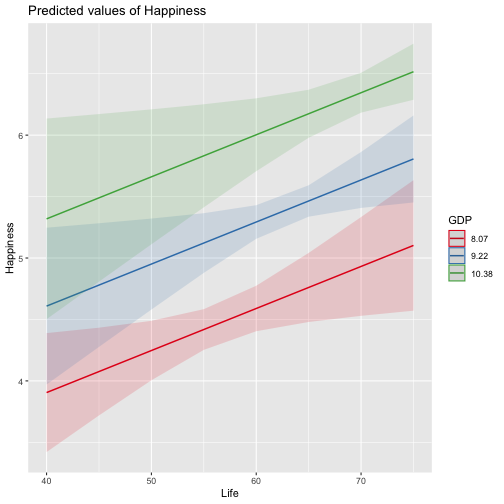<!-- --> --- ### Two continuous predictors + interaction 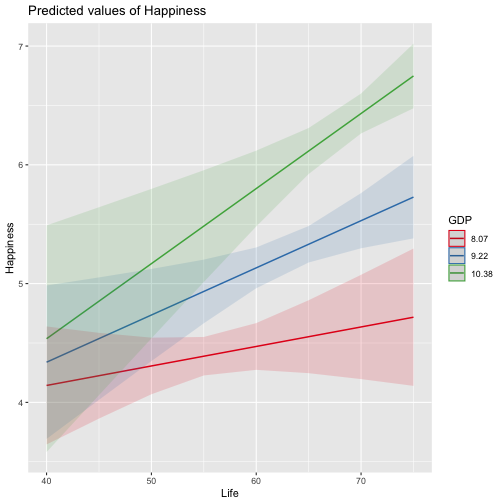<!-- --> --- ```r library(emmeans) data %>% lm(Happiness ~ Life*GDP, data = .) %>% emtrends(., var = "Life", ~GDP, at = list(GDP = c(8,9,10))) ``` ``` ## GDP Life.trend SE df lower.CL upper.CL ## 8 0.0150 0.0152 117 -0.01505 0.0451 ## 9 0.0353 0.0136 117 0.00825 0.0623 ## 10 0.0555 0.0155 117 0.02481 0.0862 ## ## Confidence level used: 0.95 ``` --- ### One categorical predictor ```r data %>% lm(Happiness ~ World, data = .) %>% summary ``` ``` ## ## Call: ## lm(formula = Happiness ~ World, data = .) ## ## Residuals: ## Min 1Q Median 3Q Max ## -2.0713 -0.4976 0.0398 0.5908 1.9147 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 6.7048 0.1572 42.646 < 2e-16 *** ## World2 -1.2876 0.2161 -5.959 2.18e-08 *** ## World3 -2.6078 0.2161 -12.069 < 2e-16 *** ## World4 -1.1716 0.1869 -6.267 4.83e-09 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.7702 on 132 degrees of freedom ## Multiple R-squared: 0.528, Adjusted R-squared: 0.5173 ## F-statistic: 49.22 on 3 and 132 DF, p-value: < 2.2e-16 ``` --- 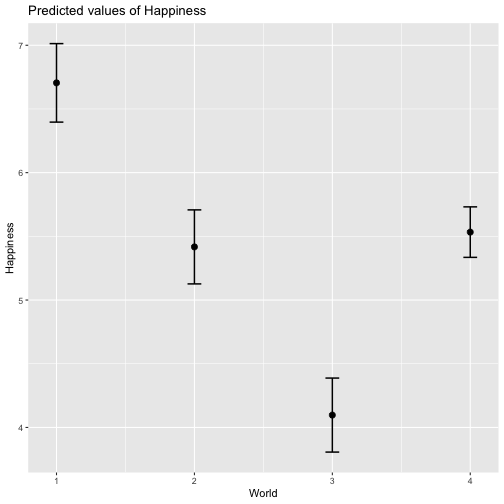<!-- --> --- ```r data %>% lm(Happiness ~ World, data = .) %>% emmeans(~World) ``` ``` ## World emmean SE df lower.CL upper.CL ## 1 6.70 0.157 132 6.39 7.02 ## 2 5.42 0.148 132 5.12 5.71 ## 3 4.10 0.148 132 3.80 4.39 ## 4 5.53 0.101 132 5.33 5.73 ## ## Confidence level used: 0.95 ``` ```r data %>% lm(Happiness ~ World, data = .) %>% summary %>% coef ``` ``` ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 6.704805 0.1572205 42.645878 4.587172e-79 ## World2 -1.287590 0.2160789 -5.958890 2.176877e-08 ## World3 -2.607793 0.2160789 -12.068710 4.620349e-23 ## World4 -1.171578 0.1869399 -6.267137 4.831268e-09 ``` --- ```r data %>% lm(Happiness ~ World, data = .) %>% emmeans(pairwise~World, adjust = "none") ``` ``` ## $emmeans ## World emmean SE df lower.CL upper.CL ## 1 6.70 0.157 132 6.39 7.02 ## 2 5.42 0.148 132 5.12 5.71 ## 3 4.10 0.148 132 3.80 4.39 ## 4 5.53 0.101 132 5.33 5.73 ## ## Confidence level used: 0.95 ## ## $contrasts ## contrast estimate SE df t.ratio p.value ## 1 - 2 1.288 0.216 132 5.959 <.0001 ## 1 - 3 2.608 0.216 132 12.069 <.0001 ## 1 - 4 1.172 0.187 132 6.267 <.0001 ## 2 - 3 1.320 0.210 132 6.298 <.0001 ## 2 - 4 -0.116 0.179 132 -0.647 0.5191 ## 3 - 4 -1.436 0.179 132 -8.004 <.0001 ``` --- ### One categorical predictor ```r data %>% lm(Happiness ~ World, data = .) %>% anova ``` ``` ## Analysis of Variance Table ## ## Response: Happiness ## Df Sum Sq Mean Sq F value Pr(>F) ## World 3 87.600 29.2001 49.221 < 2.2e-16 *** ## Residuals 132 78.308 0.5932 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` --- ### Two categorical predictors + interaction ```r data %>% lm(Happiness ~ World_simple*Hemisphere, data = .) %>% summary ``` ``` ## ## Call: ## lm(formula = Happiness ~ World_simple * Hemisphere, data = .) ## ## Residuals: ## Min 1Q Median 3Q Max ## -2.6566 -0.7113 -0.0935 0.7064 2.5165 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 5.9278 0.1502 39.473 < 2e-16 *** ## World_simple3/4 -0.9964 0.2007 -4.965 2.08e-06 *** ## HemisphereWest 0.6945 0.4053 1.713 0.089 . ## World_simple3/4:HemisphereWest -0.2677 0.4650 -0.576 0.566 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.9961 on 132 degrees of freedom ## Multiple R-squared: 0.2105, Adjusted R-squared: 0.1926 ## F-statistic: 11.73 on 3 and 132 DF, p-value: 7.291e-07 ``` --- 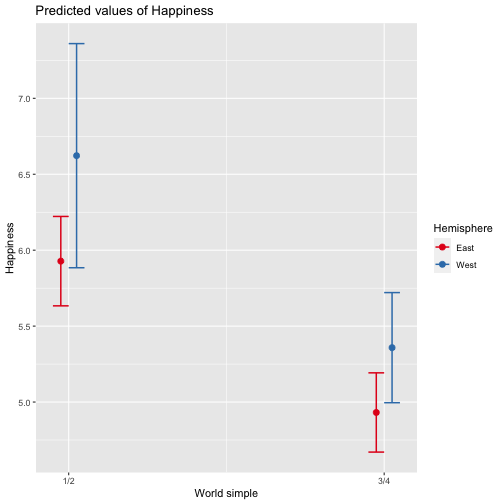<!-- --> --- ```r data %>% lm(Happiness ~ World_simple*Hemisphere, data = .) %>% emmeans(~World_simple) ``` ``` ## NOTE: Results may be misleading due to involvement in interactions ``` ``` ## World_simple emmean SE df lower.CL upper.CL ## 1/2 6.28 0.203 132 5.87 6.68 ## 3/4 5.14 0.114 132 4.92 5.37 ## ## Results are averaged over the levels of: Hemisphere ## Confidence level used: 0.95 ``` --- ```r data %>% lm(Happiness ~ World_simple*Hemisphere, data = .) %>% emmeans(~World_simple*Hemisphere) ``` ``` ## World_simple Hemisphere emmean SE df lower.CL upper.CL ## 1/2 East 5.93 0.150 132 5.63 6.22 ## 3/4 East 4.93 0.133 132 4.67 5.19 ## 1/2 West 6.62 0.377 132 5.88 7.37 ## 3/4 West 5.36 0.185 132 4.99 5.72 ## ## Confidence level used: 0.95 ``` --- ### Two categorical predictors + interaction ```r data %>% lm(Happiness ~ World_simple*Hemisphere, data = .) %>% anova ``` ``` ## Analysis of Variance Table ## ## Response: Happiness ## Df Sum Sq Mean Sq F value Pr(>F) ## World_simple 1 28.533 28.5328 28.7545 3.563e-07 *** ## Hemisphere 1 6.064 6.0639 6.1110 0.01471 * ## World_simple:Hemisphere 1 0.329 0.3288 0.3314 0.56581 ## Residuals 132 130.982 0.9923 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` -- ```r table(data$World_simple, data$Hemisphere) ``` ``` ## ## East West ## 1/2 44 7 ## 3/4 56 29 ``` --- ### Two categorical predictors + interaction ```r data %>% lm(Happiness ~ World_simple*Hemisphere, data = .) %>% car::Anova(Type = 2) ``` ``` ## Anova Table (Type II tests) ## ## Response: Happiness ## Sum Sq Df F value Pr(>F) ## World_simple 33.145 1 33.4029 5.132e-08 *** ## Hemisphere 6.064 1 6.1110 0.01471 * ## World_simple:Hemisphere 0.329 1 0.3314 0.56581 ## Residuals 130.982 132 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` --- ### Mixing categorical and continuous predictors ```r data %>% lm(Happiness ~ World + Life, data = .) %>% summary ``` ``` ## ## Call: ## lm(formula = Happiness ~ World + Life, data = .) ## ## Residuals: ## Min 1Q Median 3Q Max ## -2.17675 -0.46646 0.03876 0.53896 1.67472 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 1.85618 0.90922 2.041 0.043225 * ## World2 -0.85209 0.21255 -4.009 0.000102 *** ## World3 -1.38074 0.30051 -4.595 1.01e-05 *** ## World4 -0.61024 0.20028 -3.047 0.002801 ** ## Life 0.06775 0.01255 5.400 3.06e-07 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.701 on 130 degrees of freedom ## (1 observation deleted due to missingness) ## Multiple R-squared: 0.6146, Adjusted R-squared: 0.6027 ## F-statistic: 51.82 on 4 and 130 DF, p-value: < 2.2e-16 ``` --- 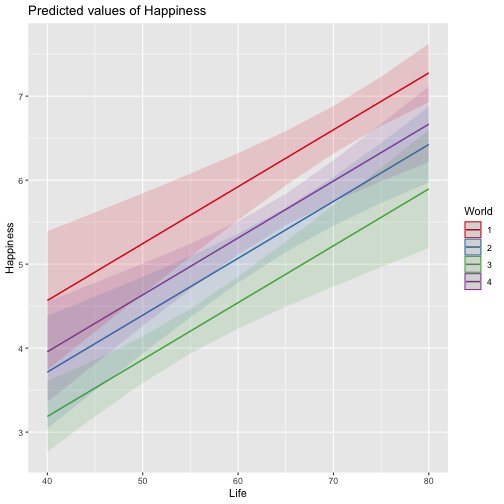<!-- --> --- ```r data %>% lm(Happiness ~ World + Life, data = .) %>% emtrends(var = "Life", ~"World") ``` ``` ## World Life.trend SE df lower.CL upper.CL ## 1 0.0678 0.0125 130 0.0429 0.0926 ## 2 0.0678 0.0125 130 0.0429 0.0926 ## 3 0.0678 0.0125 130 0.0429 0.0926 ## 4 0.0678 0.0125 130 0.0429 0.0926 ## ## Confidence level used: 0.95 ``` --- ### Mixing categorical and continuous predictors ```r data %>% lm(Happiness ~ World*Life, data = .) %>% summary ``` ``` ## ## Call: ## lm(formula = Happiness ~ World * Life, data = .) ## ## Residuals: ## Min 1Q Median 3Q Max ## -2.2068 -0.4536 0.1133 0.5345 1.3040 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 2.89645 6.04123 0.479 0.632 ## World2 1.52357 6.81397 0.224 0.823 ## World3 0.78999 6.25686 0.126 0.900 ## World4 -2.81054 6.10923 -0.460 0.646 ## Life 0.05322 0.08439 0.631 0.529 ## World2:Life -0.03791 0.09726 -0.390 0.697 ## World3:Life -0.04553 0.08969 -0.508 0.613 ## World4:Life 0.03289 0.08560 0.384 0.701 ## ## Residual standard error: 0.6911 on 127 degrees of freedom ## (1 observation deleted due to missingness) ## Multiple R-squared: 0.6341, Adjusted R-squared: 0.6139 ## F-statistic: 31.44 on 7 and 127 DF, p-value: < 2.2e-16 ``` --- 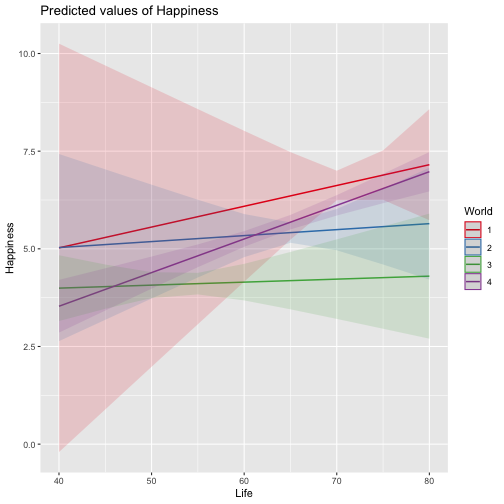<!-- --> --- ```r data %>% lm(Happiness ~ World*Life, data = .) %>% emtrends(var = "Life", ~"World") ``` ``` ## World Life.trend SE df lower.CL upper.CL ## 1 0.05322 0.0844 127 -0.1138 0.2202 ## 2 0.01531 0.0483 127 -0.0804 0.1110 ## 3 0.00768 0.0304 127 -0.0524 0.0678 ## 4 0.08611 0.0143 127 0.0578 0.1144 ## ## Confidence level used: 0.95 ``` --- ## Concept 2: Suppression .purple[Suppression] occurs when the inclusion of a covariate (X2) enhances or reverses the relationship between a predictor (X1) and outcome (Y). Example 1: `\(\hat{Y}_i = 5 + .3X1_i\)` `\(\hat{Y}_i = 3 + .7X1_i + .3X2_i\)` Example 2: `\(\hat{Y}_i = 5 + .3X1_i\)` `\(\hat{Y}_i = 3 -.4X1_i + .3X2_i\)` --- ## Suppression Why does this occur? A few reasons, but the common thread to all of these is that X1 and X2 will be correlated. Suppression can be "real" -- for example, the relation between mathematical ability and outcomes is often enhanced after controlling for verbal ability. But suppression can be an artifact -- this is most often the case when X2 _overcontrols_ X1. What to do? Check your theory and see if the finding replicates in a new sample. --- ## Concept 3: Endogeneity Endogeneity refers to a situation in which a predictor (X1) is associated with an error term (e). 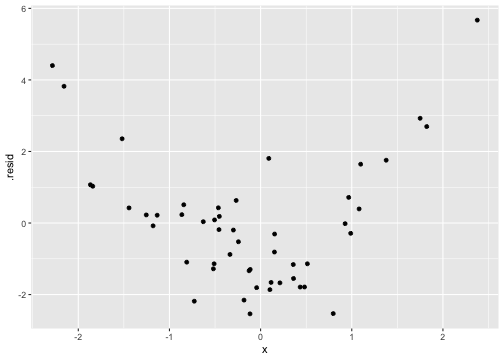<!-- --> --- ## Concept 3: Endogeneity Endogeneity refers to a situation in which a predictor (X1) is associated with an error term (e). 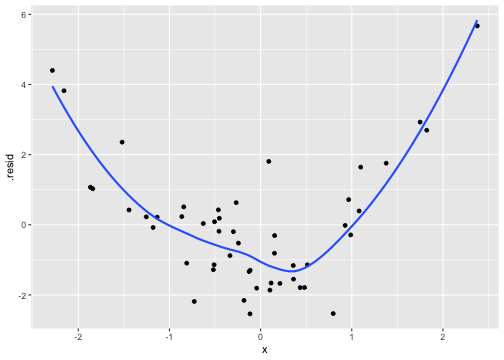<!-- --> --- class: inverse ## Lessons from machine learning Yarkoni and Westfall (2017) describe the goals of explanation and prediction in science. - Explanation: describe causal underpinnings of behaviors/outcomes - Prediction: accurately forecast behaviors/outcomes In some ways, these goals work in tandem. Good prediction can help us develop theory of explanation and vice versa. But, statistically speaking, they are in tension with one another: statistical models that accurately describe causal truths often have poor prediction and are complex; predictive models are often very different from the data-generating processes. ??? Y&W: we should spend more time and resources developing predictive models than we do not (not necessarily than explanation models, although they probably think that's true) --- ## Yarkoni and Westfall (2017) .pull-left[ .purple[Overfitting:] mistakenly fitting sample-specific noise as if it were signal - OLS models tend to be overfit because they minimize error for a specific sample .purple[Bias:] systematically over or under estimating parameters .purple[Variance:] how much estimates tend to jump around] .pull-right[ 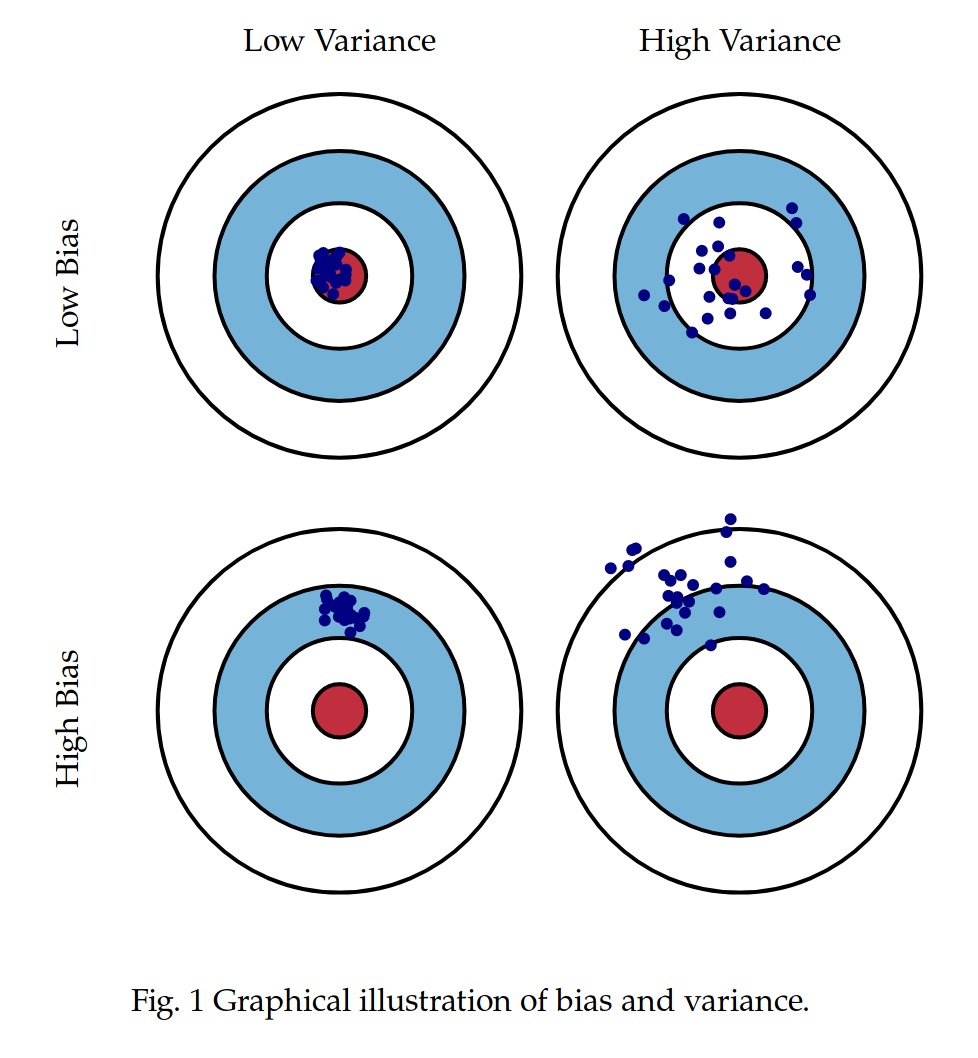 ] --- ## Yarkoni and Westfall (2017) **Big Data** * Reduce the likelihood of overfitting -- more data means less error **Cross-validation** * Is my model overfit? **Regularization** * Constrain the model to be less overfit (and more biased) --- ### Big Data Sets "Every pattern that could be observed in a given dataset reflects some... unknown combination of signal and error" (page 1104). Error is random, so it cannot correlate with anything; as we aggregate many pieces of information together, we reduce error. Thus, as we get bigger and bigger datasets, the amount of error we have gets smaller and smaller --- ### Cross-validation **Cross-validation** is a family of techniques that involve testing and training a model on different samples of data. * Replication * Hold-out samples * K-fold * Split the original dataset into 2(+) datasets, train a model on one set, test it in the other * Recycle: each dataset can be a training AND a testing; average model fit results to get better estimate of fit * Can split the dataset into more than 2 sections --- ```r library(here) stress.data = read.csv(here("data/stress.csv")) library(psych) describe(stress.data, fast = T) ``` ``` ## vars n mean sd min max range se ## id 1 118 59.50 34.21 1.00 118.00 117.00 3.15 ## Anxiety 2 118 7.61 2.49 0.70 14.64 13.94 0.23 ## Stress 3 118 5.18 1.88 0.62 10.32 9.71 0.17 ## Support 4 118 8.73 3.28 0.02 17.34 17.32 0.30 ## group 5 118 NaN NA Inf -Inf -Inf NA ``` ```r model.lm = lm(Stress ~ Anxiety*Support*group, data = stress.data) summary(model.lm)$r.squared ``` ``` ## [1] 0.4126943 ``` --- ### Example: 10-fold cross validation ```r # new package! library(caret) # set control parameters ctrl <- trainControl(method="cv", number=10) # use train() instead of lm() cv.model <- train(Stress ~ Anxiety*Support*group, data = stress.data, trControl=ctrl, # what are the control parameters method="lm") # what kind of model cv.model ``` ``` ## Linear Regression ## ## 118 samples ## 3 predictor ## ## No pre-processing ## Resampling: Cross-Validated (10 fold) ## Summary of sample sizes: 106, 106, 107, 106, 106, 107, ... ## Resampling results: ## ## RMSE Rsquared MAE ## 1.552992 0.3607622 1.26259 ## ## Tuning parameter 'intercept' was held constant at a value of TRUE ``` --- ### Regularization Penalizing a model as it grows more complex. * Usually involves shrinking coefficient estimates -- the model will fit less well in-sample but may be more predictive *lasso regression*: balance minimizing sum of squared residuals (OLS) and minimizing smallest sum of absolute values of coefficients - coefficients are more biased (tend to underestimate coefficients) but produce less variability in results [See here for a tutorial](https://www.statology.org/lasso-regression-in-r/). --- ### NHST no more Once you've imposed a shrinkage penalty on your coefficients, you've wandered far from the realm of null hypothesis significance testing. In general, you'll find that very few machine learning techniques are compatible with probability theory (including Bayesian), because they're focused on different goals. Instead of asking, "how does random chance factor into my result?", machine learning optimizes (out of sample) prediction. Both methods explicitly deal with random variability. In NHST and Bayesian probability, we're trying to estimate the degree of randomness; in machine learning, we're trying to remove it. --- ## Summary: Yarkoni and Westfall (2017) **Big Data** * Reduce the likelihood of overfitting -- more data means less error **Cross-validation** * Is my model overfit? **Regularization** * Constrain the model to be less overfit --- class: inverse ## Next time... PSY 613 with Elliot Berkman! .small[(But first take the final quiz.)]