Univariate regression III

class: center, middle, inverse, title-slide

# Univariate regression III

---

## Last week

.pull-left[

**Unstandardized regression equation**

`$$Y = b_0 + b_1X + e$$`

- Intercept and slope are interpreted in the units of Y.
  - Useful if the units of Y are meaningful.
  
- Built from covariances and variances

`$$b_1 = \frac{cov_{XY}}{s^2_X}$$`

]

.pull-right[

**Standardized regression equation**

`$$Z_Y = b^*_1Z_X + e$$`

- Slope are interpreted in standardized units.
  - Useful for comparison
  
- Built from correlations

`$$b^*_1 = r_{xy}$$`

]

---

## Last week -- Inferential tests

.pull-left[
**Omnibus test**

- Does the model fit the data?

- *F*-test (ratio of variances)

- How many magnitudes larger is variability attributed to the model compared to left-over variability?
    
* Effect size: Model fit can be measured in terms of `$\large R^2$` or `$\large s_{Y|X}$`
  ]

---
## Terminology

- `$R^2$`
--
  - .purple[coefficient of determination]
  - squared correlation between `$Y$` and `$\hat{Y}$`
  - proportion of variance in Y accounted for by the model
  
- `$s_{Y|X}$`

--
  - .purple[standard error of the estimate] and the square root of the .purple[mean square error (MSE)] 
  - measure of discrepancy between model and data
  - MSE: variance around fitted regression line

---

## Example
 
*Overclaiming* occurs when people claim that they know something that is impossible to know; are experts susceptible to overclaiming?

Participants completed a measure of **_self-perceived knowledge_**, in which they indicate their level of knowledge in the area of personal finance. Next participants indicated how much they knew about 15 terms related to personal finance (e.g., home equity). Included in the 15 items were three terms that do not actually exist (e.g., annualized credit). Thus, **_overclaiming_** occurred when participants said that they were knowledgeable about the non-existent terms.

.small[
Atir, S., Rosenzweig, E., & Dunning, D. (2015). [When knowledge knows no bounds: Self-perceived expertise predicts claims of impossible knowledge.](https://journals.sagepub.com/stoken/default+domain/ZtrwAQcGwtzhkvv8vgKq/full) Psychological Science, 26, 1295-1303. ]

---

```r
library(here)
expertise = read.csv(here("data/expertise.csv"))
psych::describe(expertise)
```

```
##                          vars   n   mean    sd median trimmed   mad   min
## id                          1 202 101.50 58.46 101.50  101.50 74.87  1.00
## order_of_tasks              2 202   1.50  0.50   1.50    1.50  0.74  1.00
*## self_perceived_knowledge    3 202   4.43  1.17   4.50    4.45  0.74  1.00
*## overclaiming_proportion     4 202   0.31  0.23   0.28    0.29  0.25  0.00
## accuracy                    5 202   0.30  0.21   0.28    0.29  0.21 -0.19
## FINRA_score                 6 202   3.70  1.19   4.00    3.85  1.48  0.00
##                             max  range  skew kurtosis   se
## id                       202.00 201.00  0.00    -1.22 4.11
## order_of_tasks             2.00   1.00  0.00    -2.01 0.04
## self_perceived_knowledge   7.00   6.00 -0.20     0.15 0.08
## overclaiming_proportion    1.00   1.00  0.64    -0.31 0.02
## accuracy                   0.93   1.12  0.28    -0.07 0.01
## FINRA_score                5.00   5.00 -1.01     0.57 0.08
```

```r
cor(expertise[,c("self_perceived_knowledge", "overclaiming_proportion")])
```

```
##                          self_perceived_knowledge overclaiming_proportion
## self_perceived_knowledge                1.0000000               0.4811502
## overclaiming_proportion                 0.4811502               1.0000000
```

---

```r
fit.1 = lm(overclaiming_proportion ~ self_perceived_knowledge, 
           data = expertise)
anova(fit.1)
```

```
## Analysis of Variance Table
## 
## Response: overclaiming_proportion
##                           Df Sum Sq Mean Sq F value             Pr(>F)    
## self_perceived_knowledge   1 2.5095 2.50948  60.249 0.0000000000004225 ***
## Residuals                200 8.3303 0.04165                               
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

---

```r
summary(fit.1)
```

```
## 
## Call:
## lm(formula = overclaiming_proportion ~ self_perceived_knowledge, 
##     data = expertise)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.50551 -0.15610  0.00662  0.12167  0.54215 
## 
## Coefficients:
##                          Estimate Std. Error t value          Pr(>|t|)    
## (Intercept)              -0.11406    0.05624  -2.028            0.0439 *  
## self_perceived_knowledge  0.09532    0.01228   7.762 0.000000000000422 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2041 on 200 degrees of freedom
## Multiple R-squared:  0.2315,	Adjusted R-squared:  0.2277 
## F-statistic: 60.25 on 1 and 200 DF,  p-value: 0.0000000000004225
```

---

```r
library(sjPlot)
set_theme(base = theme_bw())
```

.pull-left[

```r
plot_model(fit.1, 
           type = "pred", 
           show.data = T) 
```

![](5-regression_files/figure-html/unnamed-chunk-7-1.png)
]

.pull-right[

```r
plot_model(fit.1, 
           type = "pred", show.data = T, 
           jitter = T) 
```

![](5-regression_files/figure-html/unnamed-chunk-8-1.png)
]

???

Point out here:
* Can be hard to visualize data when you have a Likert scale or other measure with a relatively small number of possible answers. 
* BUT jitter can produce impossible data points and possibly hide floor or ceiling effects. 
---

## regression coefficient

`$$\Large H_{0}: \beta_{1}= 0$$`
`$$\Large H_{1}: \beta_{1} \neq 0$$`

---

## What does the regression coefficient test?

- Does X provide any predictive information?

- Does X provide any explanatory power regarding the variability of Y?

- Is the the average value different from the best guess 
  - (i.e., is `$\bar{Y}$` equal to `$\hat{Y}$` ?)

- Is the regression line not flat?

- Are X and Y correlated?

---

## Regression coefficient
`$$\Large se_{b} = \frac{s_{Y}}{s_{X}}{\sqrt{\frac {1-r_{xy}^2}{n-2}}}$$`
`$$\Large t(n-2) = \frac{b_{1}}{se_{b}}$$`

---

```r
summary(fit.1)
```

```
## 
## Call:
## lm(formula = overclaiming_proportion ~ self_perceived_knowledge, 
##     data = expertise)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.50551 -0.15610  0.00662  0.12167  0.54215 
## 
## Coefficients:
##                          Estimate Std. Error t value          Pr(>|t|)    
## (Intercept)              -0.11406    0.05624  -2.028            0.0439 *  
*## self_perceived_knowledge  0.09532    0.01228   7.762 0.000000000000422 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2041 on 200 degrees of freedom
## Multiple R-squared:  0.2315,	Adjusted R-squared:  0.2277 
## F-statistic: 60.25 on 1 and 200 DF,  p-value: 0.0000000000004225
```

---

## `$se_b$`

- .purple[standard error for the slope coefficient]

- represent our uncertainty (noise) in our estimate of the regression coefficient 
- different from (but proportional to) the standard error of the estimate

-  we can take our estimate `$(b)$` and put confidence regions around it to get an estimate of what could be "possible" if we ran the study again

---
## Intercept

- more complex standard error calculation

- the calculation depends on how far the X value (here zero) is away from the mean of X

- farther from the mean, less information, thus more uncertainty 
    
- we'll come back to this calculation shortly
    
---

```r
summary(fit.1)
```

```
## 
## Call:
## lm(formula = overclaiming_proportion ~ self_perceived_knowledge, 
##     data = expertise)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.50551 -0.15610  0.00662  0.12167  0.54215 
## 
## Coefficients:
##                          Estimate Std. Error t value          Pr(>|t|)    
*## (Intercept)              -0.11406    0.05624  -2.028            0.0439 *  
## self_perceived_knowledge  0.09532    0.01228   7.762 0.000000000000422 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2041 on 200 degrees of freedom
## Multiple R-squared:  0.2315,	Adjusted R-squared:  0.2277 
## F-statistic: 60.25 on 1 and 200 DF,  p-value: 0.0000000000004225
```

---
## Confidence interval for coefficients

- same equation as we've been working with:

`$$CI_b = b \pm CV(se_b)$$`

- How do we estimate the critical value?

---

```r
coef(summary(fit.1))
```

```
##                             Estimate Std. Error   t value              Pr(>|t|)
## (Intercept)              -0.11405571 0.05624236 -2.027932 0.0438935615758865028
## self_perceived_knowledge  0.09531747 0.01227997  7.762029 0.0000000000004224832
```

```r
confint(fit.1)
```

```
##                                2.5 %       97.5 %
## (Intercept)              -0.22495982 -0.003151603
## self_perceived_knowledge  0.07110265  0.119532290
```

`$b_1 \pm CV(se_b) = 0.095 \pm 1.972(0.012)$`
`$b_1 \pm CV(se_b) = 0.095 \pm 0.024$`

---
## `$se_{\hat{Y_i}}$`

In addition to estimating precision around the our coefficients, we can also estimate our precision around our predicted values, `$\hat{Y_i}$`. Why might this be a useful exercise?

The formula to estimate the standard error of any particular `$\hat{Y_i}$` is

`$$se_{\hat{Y}_i} = s_{Y|X}*\sqrt{\frac {1}{n}+\frac{(X_i-\bar{X})^2}{(n-1)s_{X}^2}}$$`
---

```r
library(broom)
model_info = augment(fit.1, se_fit = T)
psych::describe(model_info, fast=T)
```

```
##                          vars   n mean   sd   min  max range   se
## overclaiming_proportion     1 202 0.31 0.23  0.00 1.00  1.00 0.02
## self_perceived_knowledge    2 202 4.43 1.17  1.00 7.00  6.00 0.08
## .fitted                     3 202 0.31 0.11 -0.02 0.55  0.57 0.01
*## .se.fit                     4 202 0.02 0.01  0.01 0.04  0.03 0.00
## .resid                      5 202 0.00 0.20 -0.51 0.54  1.05 0.01
## .hat                        6 202 0.01 0.01  0.00 0.05  0.04 0.00
## .sigma                      7 202 0.20 0.00  0.20 0.20  0.00 0.00
## .cooksd                     8 202 0.01 0.01  0.00 0.09  0.09 0.00
## .std.resid                  9 202 0.00 1.00 -2.50 2.68  5.18 0.07
```

```r
head(model_info[,c(".fitted", ".se.fit")])
```

```
## # A tibble: 6 × 2
##   .fitted .se.fit
##     <dbl>   <dbl>
## 1   0.410  0.0195
## 2   0.315  0.0144
## 3   0.220  0.0183
## 4   0.458  0.0241
## 5   0.124  0.0277
## 6   0.553  0.0347
```

We can string these together in a figure and create **confidence bands**.
---

![](5-regression_files/figure-html/unnamed-chunk-15-1.png)
---

![](5-regression_files/figure-html/unnamed-chunk-16-1.png)
---

![](5-regression_files/figure-html/unnamed-chunk-17-1.png)

---

Let's return to the idea of the uncertainty around our slope and intercept estimates.

```r
confint(fit.1)
```

```
##                                2.5 %       97.5 %
## (Intercept)              -0.22495982 -0.003151603
## self_perceived_knowledge  0.07110265  0.119532290
```

We accept that these ranges represent our guess for where the true values of these parameters could be. So while we estimated a single slope and single intercept, reasonably, there is a set of slopes and intercepts that we would consider reasonable.

What if we took the extremes from these distributions?

`$\hat{Y}_i = -0.22 + 0.12X_i$`

`$\hat{Y}_i = 0 + 0.07X_i$`

---

![](5-regression_files/figure-html/unnamed-chunk-20-1.png)

---

![](5-regression_files/figure-html/unnamed-chunk-21-1.gif)

---
## Confidence Bands for regression line
![](5-regression_files/figure-html/unnamed-chunk-22-1.png)
---
Compare mean estimate for self-perceived knowledge based on regression vs binning

![](5-regression_files/figure-html/unnamed-chunk-23-1.png)
---
## Confidence Bands

`$$\Large \hat{Y}\pm t_{critical} * s_{Y|X}*\sqrt{\frac {1}{n}+\frac{(X-\bar{X})^2}{(n-1)s_{X}^2}}$$`

---
## Prediction bands

`$$\large \hat{Y}\pm t_{critical} * s_{Y|X}*\sqrt{1+ \frac {1}{n}+\frac{(X-\bar{X})^2}{(n-1)s_{X}^2}}$$`

- predicting and individual `$i's$` score, not the `$\hat{Y}$` for a particular level of X. (A new `$Y_i$` given `$X_i$`, rather than `$\bar{Y}$` given `$X_i$` )

- Because there is greater variation in predicting an individual value rather than a mean, the prediction band is greater

- Combines unknown variability of the estimated mean `$(\text{as reflected in }se_b)$` with peoples' scores around mean `$(\text{standard error of the estimate }, s_{Y|X})$`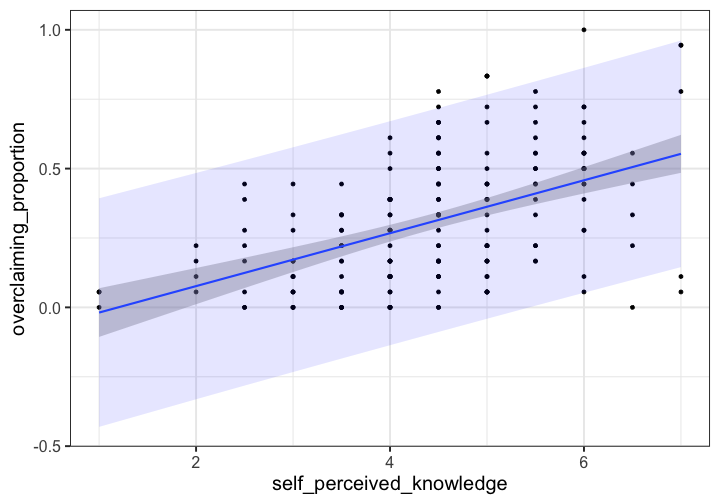

---

![](5-regression_files/figure-html/unnamed-chunk-24-1.png)

---
class: inverse

## Model comparison

One final way to statistically test the fit of our model.

---
## Model comparison

- The basic idea is asking how much variance remains unexplained in our model. This "left over" variance can be contrasted with an alternative model/hypothesis. We can ask does adding a new predictor variable help explain more variance or should we stick with a parsimonious model.

- Every test of an omnibus model is implicitly a model comparisons, typically of your fitted model with the nil model (no slopes). This framework allows you to be more flexible and explicit.

---

```r
fit.1 <- lm(overclaiming_proportion ~ self_perceived_knowledge, 
            data = expertise)

fit.0 <- lm(overclaiming_proportion ~ 1,
            data = expertise)
```

---

```r
summary(fit.0)
```

```
## 
## Call:
## lm(formula = overclaiming_proportion ~ 1, data = expertise)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.30803 -0.19692 -0.03025  0.13641  0.69197 
## 
## Coefficients:
##             Estimate Std. Error t value            Pr(>|t|)    
## (Intercept)  0.30803    0.01634   18.85 <0.0000000000000002 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2322 on 201 degrees of freedom
```

---

```r
summary(fit.1)
```

---

```r
anova(fit.0)
```

```
## Analysis of Variance Table
## 
## Response: overclaiming_proportion
##            Df Sum Sq  Mean Sq F value Pr(>F)
## Residuals 201  10.84 0.053929
```

---

```r
anova(fit.1)
```

---

```r
anova(fit.1, fit.0)
```

```
## Analysis of Variance Table
## 
## Model 1: overclaiming_proportion ~ self_perceived_knowledge
## Model 2: overclaiming_proportion ~ 1
##   Res.Df     RSS Df Sum of Sq      F             Pr(>F)    
## 1    200  8.3303                                           
## 2    201 10.8398 -1   -2.5095 60.249 0.0000000000004225 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
---
## Model Comparisons

- Model comparisons are redundant with nil/null hypotheses and coefficient tests right now, but will be more flexible down the road.

- Key is to start thinking about your implicit alternative models

- The ultimate goal would be to create two models that represent two equally plausible theories.

- Theory A is made up of components XYZ, whereas theory B has QRS components. You can then ask which theory (model) is better?

---
class: inverse

## Next time

The general linear model