Multiple Regression

class: center, middle, inverse, title-slide

# Multiple Regression

---

## Last time

- Semi-partial and partial correlations

## Today

- Introduction to multiple regression

---

## Regression equation

`$$\large \hat{Y} = b_0 + b_1X_1 + b_2X_2 + \dots+b_kX_k$$`

- regression coefficients are "partial" regression coefficients

- predicted change in `$Y$` for a 1 unit change in `$X$`, .purple[holding all other predictors constant]
  
  - similar in interpretation to semi-partial correlation -- represents contribution to all of Y from unique part of each `$X$`
  
  - same statistical test as partial correlation -- unique variance of `$Y$` explained by unique variance of each `$X$`

---

## example

```r
library(here); library(tidyverse)
support_df = read.csv(here("data/support.csv")) 
library(psych)
describe(support_df, fast = T)
```

```
##                 vars  n mean   sd  min  max range   se
## give_support       1 78 4.99 1.07 2.77 7.43  4.66 0.12
## receive_support    2 78 7.88 0.85 5.81 9.68  3.87 0.10
## relationship       3 78 5.85 0.86 3.27 7.97  4.70 0.10
```

```r
round(cor(support_df),2)
```

```
##                 give_support receive_support relationship
## give_support            1.00            0.39         0.36
## receive_support         0.39            1.00         0.45
## relationship            0.36            0.45         1.00
```

---

## example

```r
mr.model <- lm(relationship ~ receive_support + give_support, data = support_df)
summary(mr.model)
```

```
...
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)   
## (Intercept)      2.07212    0.81218   2.551  0.01277 * 
## receive_support  0.37216    0.11078   3.359  0.00123 **
## give_support     0.17063    0.08785   1.942  0.05586 . 
...
```

```r
# partial correlation tests
with(support_df, ppcor::pcor.test(relationship, receive_support, give_support))
```

```
##    estimate     p.value statistic  n gp  Method
## 1 0.3616442 0.001230843  3.359301 78  1 pearson
```

```r
with(support_df, ppcor::pcor.test(relationship, give_support, receive_support))
```

```
##   estimate    p.value statistic  n gp  Method
## 1 0.218838 0.05585914  1.942271 78  1 pearson
```
???

If a univariate regression is estimating the best-fit line, what is this estimating?

---
## Visualizing multiple regression

```r
library(visreg)

visreg2d(mr.model,"receive_support", "give_support", plot.type = "persp")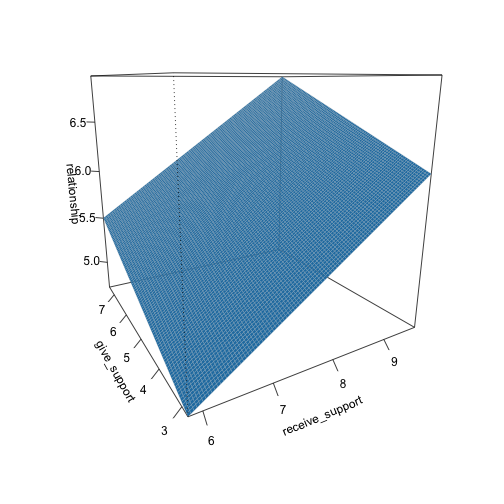
```

![](8-m_regression_files/figure-html/unnamed-chunk-5-1.png)

---

## Calculating coefficients

Just like with univariate regression, we calculate the OLS solution. As a reminder, this calculation will yield the estimate that reduces the sum of the squared deviations from the line:

.pull-left[
### Unstandardized
`$$\large \hat{Y} = b_0 + b_{1}X1 + b_{2}X_2$$`
$$\large \text{minimize} \sum (Y-\hat{Y})^2 $$
]
.pull-right[

### Standardized
`$$\large \hat{Z}_{Y} = b_{1}^*Z_{X1} + b_{2}^*Z_{X2}$$`
`$$\large \text{minimize} \sum (z_{Y}-\hat{z}_{Y})^2$$`
]

---
## Calculating the standardized regression coefficient

`$$b_{1}^* = \frac{r_{Y1}-r_{Y2}r_{12}}{1-r_{12}^2}$$`

`$$b_{2}^* = \frac{r_{Y2}-r_{Y1}r_{12}}{1-r_{12}^2}$$`

---

## Relationships between partial, semi- and `$b*$`

(Standardized) Regression coefficients, partial correlations, and semi-partial correlations are all ways to represent the relationship between two variables while taking into account a third (or more!) variables.

- Each is a standardized effect, meaning the effect size is calculated in standardized units, bounded by -1 and 1*. This means they can be compared across studies, metrics, etc.

Note, however, that the calculations differ between the three effect sizes. These effect sizes are not synonymous and often yield different answers.

- if predictors are not correlated, `$r$`,  `$sr$` `$(r_{Y(1.2)})$` and `$b*$` are equal

.small[*Actually, standardized regression coefficients are not bounded by -1 and 1, but it's rare to see values this large, and [usually indicative of some multicollinearity](http://www.statmodel.com/download/Joreskog.pdf).]
---

** Standardized multiple regression coefficient** `$b^*$`

`$$\large \frac{r_{Y1}-r_{Y2}r_{12}}{1-r_{12}^2}$$`

** Semi-partial correlation** `$r_{y(1.2)}$`
`$$\large \frac{r_{Y1}-r_{Y2}r_{Y12} }{\sqrt{1-r_{12}^2}}$$`

** Partial correlation** `$r_{y1.2}$`
`$$\large \frac{r_{Y1}-r_{Y2}r_{{12}}}{\sqrt{1-r^2_{Y2}}\sqrt{1-r^2_{12}}}$$`

---

```r
support_df = support_df %>%
  mutate(z_give_support = scale(give_support),
         z_receive_support = scale(receive_support),
         z_relationship = scale(relationship))

mod0 = lm(z_relationship ~ z_give_support + z_receive_support, 
          data = support_df)

round(coef(mod0),3)
```

```
##       (Intercept)    z_give_support z_receive_support 
##             0.000             0.212             0.367
```

.pull-left[

```r
spcor.test(x = support_df$relationship, 
           y = support_df$give_support, 
           z = support_df$receive_support)$estimate
```

```
## [1] 0.1953065
```
]

.pull-right[

```r
pcor.test(x = support_df$relationship, 
          y = support_df$give_support, 
          z = support_df$receive_support)$estimate
```

```
## [1] 0.218838
```

]
---
    
## Original metric

`$$b_{1} = b_{1}^*\frac{s_{Y}}{s_{X1}}$$`

`$$b_{1}^* = b_{1}\frac{s_{X1}}{s_{Y}}$$`

### Intercept

`$$b_{0} = \bar{Y} - b_{1}\bar{X_{1}} - b_{2}\bar{X_{2}}$$`
---

```r
mr.model <- lm(relationship ~ receive_support + give_support, data = support_df)
summary(mr.model)
```

```
## 
## Call:
## lm(formula = relationship ~ receive_support + give_support, data = support_df)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.26837 -0.40225  0.07701  0.42147  1.76074 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)   
*## (Intercept)      2.07212    0.81218   2.551  0.01277 * 
## receive_support  0.37216    0.11078   3.359  0.00123 **
## give_support     0.17063    0.08785   1.942  0.05586 . 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.7577 on 75 degrees of freedom
## Multiple R-squared:  0.2416,	Adjusted R-squared:  0.2214 
## F-statistic: 11.95 on 2 and 75 DF,  p-value: 0.00003128
```

---

```r
mr.model <- lm(relationship ~ receive_support + give_support, data = support_df)
summary(mr.model)
```

```
## 
## Call:
## lm(formula = relationship ~ receive_support + give_support, data = support_df)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.26837 -0.40225  0.07701  0.42147  1.76074 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)   
## (Intercept)      2.07212    0.81218   2.551  0.01277 * 
*## receive_support  0.37216    0.11078   3.359  0.00123 **
*## give_support     0.17063    0.08785   1.942  0.05586 . 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.7577 on 75 degrees of freedom
## Multiple R-squared:  0.2416,	Adjusted R-squared:  0.2214 
## F-statistic: 11.95 on 2 and 75 DF,  p-value: 0.00003128
```

---

## "Controlling for"

![](images/control.gif)

Taken from [@nickchk](https://twitter.com/nickchk)

---

## Compare the slopes

```r
un.model <- lm(relationship ~ give_support,           data = support_df)
summary(un.model)
```

```
...
## Coefficients:
##              Estimate Std. Error t value            Pr(>|t|)    
## (Intercept)   4.42369    0.43882  10.081 0.00000000000000117 ***
*## give_support  0.28681    0.08605   3.333             0.00133 ** 
...
```

```r
mr.model <- lm(relationship ~ receive_support + give_support, data = support_df)
summary(mr.model)
```

```
...
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)   
## (Intercept)      2.07212    0.81218   2.551  0.01277 * 
## receive_support  0.37216    0.11078   3.359  0.00123 **
*## give_support     0.17063    0.08785   1.942  0.05586 . 
...
```

---

```r
library(sjPlot)
plot_model(un.model, type = "pred", terms = c("give_support")) + ylim(4.5, 7.5)
```

![](8-m_regression_files/figure-html/unnamed-chunk-13-1.png)

---

```r
library(sjPlot)
plot_model(mr.model, type = "pred", terms = c("give_support")) + ylim(4.5, 7.5)
```

![](8-m_regression_files/figure-html/unnamed-chunk-14-1.png)

---

![](8-m_regression_files/figure-html/unnamed-chunk-15-1.png)

---

![](8-m_regression_files/figure-html/unnamed-chunk-16-1.png)

---

### Predictions: univariate model

![](8-m_regression_files/figure-html/unnamed-chunk-17-1.png)

---

### Predictions: multiple regression model

![](8-m_regression_files/figure-html/unnamed-chunk-18-1.png)

---

```r
plot_model(mr.model, type = "pred", 
           terms = c("give_support", "receive_support[meansd]"))
```

![](8-m_regression_files/figure-html/unnamed-chunk-19-1.png)

---

Even though the slope of one predictor, `give_support`, is less steep (accounting for less variance), the model overall captures more of the variability in Y (relationship quality).

```r
un.model <- lm(relationship ~ give_support, data = support_df)
summary(un.model)
```

```
...
## Residual standard error: 0.8073 on 76 degrees of freedom
## Multiple R-squared:  0.1275,	Adjusted R-squared:  0.1161 
## F-statistic: 11.11 on 1 and 76 DF,  p-value: 0.001329
...
```

```r
mr.model <- lm(relationship ~ give_support + receive_support, data = support_df)
summary(mr.model)
```

```
...
## Residual standard error: 0.7577 on 75 degrees of freedom
## Multiple R-squared:  0.2416,	Adjusted R-squared:  0.2214 
## F-statistic: 11.95 on 2 and 75 DF,  p-value: 0.00003128
...
```

---

## Estimating model fit

```r
mr.model <- lm(relationship ~ receive_support + give_support, data = support_df)
summary(mr.model)
```

```
## 
## Call:
## lm(formula = relationship ~ receive_support + give_support, data = support_df)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.26837 -0.40225  0.07701  0.42147  1.76074 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)   
## (Intercept)      2.07212    0.81218   2.551  0.01277 * 
## receive_support  0.37216    0.11078   3.359  0.00123 **
## give_support     0.17063    0.08785   1.942  0.05586 . 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.7577 on 75 degrees of freedom
*## Multiple R-squared:  0.2416,	Adjusted R-squared:  0.2214 
## F-statistic: 11.95 on 2 and 75 DF,  p-value: 0.00003128
```

---

```r
library(broom); library(scales)
support_df1 = augment(mr.model)
support_df1 %>%
  ggplot(aes(x = relationship, y = .fitted)) + geom_point() + geom_hline(aes(yintercept = mean(relationship), color = "bar(Y)")) + geom_smooth(method = "lm", aes(color = "R[bar(Y)][Y]")) + scale_x_continuous("Y (relationship)") + scale_color_discrete(labels = parse_format()) + scale_y_continuous(expression(hat(Y))) + theme_bw(base_size = 20)
```

![](8-m_regression_files/figure-html/unnamed-chunk-23-1.png)

---
## Multiple correlation, R

`$$\large \hat{Y} = b_{0} + b_{1}X_{1} + b_{2}X_{2}$$`

- `$\hat{Y}$` is a linear combination of Xs
- `$r_{Y\hat{Y}}$` = multiple correlation = R

`$$\large R = \sqrt{b_{1}^*r_{Y1} + b_{2}^*r_{Y2}}$$`
`$$\large R^2 = {b_{1}^*r_{Y1} + b_{2}^*r_{Y2}}$$`

---

![](images/venn/Slide7.jpeg)
---

![](images/venn/Slide8.jpeg)

---
## Decomposing sums of squares

We haven't changed our method of decomposing variance from the univariate model

`$$\Large \frac{SS_{regression}}{SS_{Y}} = R^2$$`
`$$\Large {SS_{regression}} = R^2({SS_{Y})}$$`

`$$\Large {SS_{residual}} = (1- R^2){SS_{Y}}$$`
  
---

## significance tests

- `$R^2$` (omnibus)  
- Regression Coefficients  
- Increments to `$R^2$`  
    
---

## R-squared, `$R^2$`

- Same interpretation as before

- Adding predictors into your model will increase `$R^2$` – regardless of whether or not the predictor is significantly correlated with Y.

- Think back to sampling error. If the population correlation, `$\rho$`, is 0, will your sample estimate always be 0?

- Adjusted/Shrunken `$R^2$` takes into account the number of predictors in your model

---

## Adjusted R-squared, `$\text{Adj } R^2$`

`$$\large R_{A}^2 = 1 - (1 -R^2)\frac{n-1}{n-p-1}$$`

- What happens if you add many IV's to your model that are uncorrelated with your DV?

- What happens as you add more covariates to your model that are highly correlated with your key predictor, X?

`$$b_{1}^* = \frac{r_{Y1}-r_{Y2}r_{12}}{1-r_{12}^2}$$`

---

## ANOVA

```r
summary(mr.model)
```

```
## 
## Call:
## lm(formula = relationship ~ receive_support + give_support, data = support_df)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.26837 -0.40225  0.07701  0.42147  1.76074 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)   
## (Intercept)      2.07212    0.81218   2.551  0.01277 * 
## receive_support  0.37216    0.11078   3.359  0.00123 **
## give_support     0.17063    0.08785   1.942  0.05586 . 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.7577 on 75 degrees of freedom
## Multiple R-squared:  0.2416,	Adjusted R-squared:  0.2214 
*## F-statistic: 11.95 on 2 and 75 DF,  p-value: 0.00003128
```
---

## ANOVA

The omnibus test uses all SS associated with predictors.

```r
anova(mr.model)
```

```
## Analysis of Variance Table
## 
## Response: relationship
##                 Df Sum Sq Mean Sq F value    Pr(>F)    
*## receive_support  1 11.553 11.5528 20.1253 0.0000257 ***
*## give_support     1  2.166  2.1655  3.7724   0.05586 .  
## Residuals       75 43.053  0.5740                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

`$$SS_{\text{model}} = 13.72$$`
`$$MS_{\text{model}} = \frac{SS_{\text{model}}}{df_{\text{model}}} = 6.86$$`
`$$F_{\text{model}} = \frac{MS_{\text{model}}}{MS_{\text{residual}}} = 11.95$$`
---

## ANOVA

The omnibus test uses all SS associated with predictors.

```r
anova(mr.model)
```

Note that the _p_-values in this table do NOT match the _p_-values in the regression summary table. For the time being, just know that, in a multiple regression framework, you should use the `summary()` output to interpret the unique contribution of predictors, not the `anova()` output. We'll return to these calculations later in the term and discuss them in more detail. 
---

```r
summary(mr.model)
```

```
## 
## Call:
## lm(formula = relationship ~ receive_support + give_support, data = support_df)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.26837 -0.40225  0.07701  0.42147  1.76074 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)   
## (Intercept)      2.07212    0.81218   2.551  0.01277 * 
*## receive_support  0.37216    0.11078   3.359  0.00123 **
*## give_support     0.17063    0.08785   1.942  0.05586 . 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.7577 on 75 degrees of freedom
## Multiple R-squared:  0.2416,	Adjusted R-squared:  0.2214 
## F-statistic: 11.95 on 2 and 75 DF,  p-value: 0.00003128
```

---

## Standard errors

`$$\Large H_{0}: \beta_{X}= 0$$`
`$$\Large H_{1}: \beta_{X} \neq 0$$`

---

## Standard error of regression coefficient

In the case of univariate regression:

`$$\Large se_{b} = \frac{s_{Y}}{s_{X}}{\sqrt{\frac {1-r_{xy}^2}{n-2}}}$$`

In the case of multiple regression:

`$$\Large se_{b} = \frac{s_{Y}}{s_{X}}{\sqrt{\frac {1-R_{Y\hat{Y}}^2}{n-p-1}}} \sqrt{\frac {1}{1-R_{i.jkl...p}^2}}$$`

- As N increases... 
- As variance explained increases...

---

`$$se_{b} = \frac{s_{Y}}{s_{X}}{\sqrt{\frac {1-R_{Y\hat{Y}}^2}{n-p-1}}} \sqrt{\frac {1}{1-R_{i.jkl...p}^2}}$$`

## Tolerance

`$$1-R_{i.jkl...p}^2$$`

- Proportion of `$X_i$` that does not overlap with other predictors.
    - Bounded by 0 and 1

- Large tolerance (little overlap) means standard error will be small.

- what does this mean for including a lot of variables in your model?

---

## Tolerance in `R`

```r
library(olsrr)

ols_vif_tol(mr.model)
```

```
##         Variables Tolerance      VIF
## 1 receive_support 0.8450326 1.183386
## 2    give_support 0.8450326 1.183386
```

Why are tolerance values identical here?

---

## Which variables to include

- You goal should be to match the population model (theoretically)

- Including many variables will not bias parameter estimates but will potentially increase degrees of freedom and standard errors; in other words, putting too many variables in your model may make it _more difficult_ to find a statistically significant result

- But that's only the case if you add variables unrelated to Y or X; there are some cases in which adding the wrong variables can lead to spurious results. [Stay tuned for the lecture on causal models.]

---

## Suppression

Normally our standardized partial regression coefficients fall between 0 and `$r_{Y1}$`. However, it is possible for `$b^*_{Y1}$` to be larger than `$r_{Y1}$`. We refer to this phenomenon as .purple[suppression.]

* A non-significant `$r_{Y1}$` can become a significant `$b^*_{Y1}$` when additional variables are added to the model.

* A *positive* `$r_{Y1}$` can become a *negative* and significant `$b^*_{Y1}$`.

---

```r
stress_df = read.csv(here("data/stress.csv")) %>% dplyr::select(-id, -group)

cor(stress_df) %>% round(2)
```

```
##         Anxiety Stress Support
## Anxiety    1.00  -0.05   -0.55
## Stress    -0.05   1.00    0.52
## Support   -0.55   0.52    1.00
```

---

```r
lm(Stress ~ Anxiety, data = stress_df) %>% summary
```

```
## 
## Call:
## lm(formula = Stress ~ Anxiety, data = stress_df)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -4.580 -1.338  0.130  1.047  4.980 
## 
## Coefficients:
##             Estimate Std. Error t value            Pr(>|t|)    
## (Intercept)  5.45532    0.56017   9.739 <0.0000000000000002 ***
## Anxiety     -0.03616    0.06996  -0.517               0.606    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.882 on 116 degrees of freedom
## Multiple R-squared:  0.002297,	Adjusted R-squared:  -0.006303 
## F-statistic: 0.2671 on 1 and 116 DF,  p-value: 0.6063
```

---

```r
lm(Stress ~ Anxiety + Support, data = stress_df) %>% summary
```

```
## 
## Call:
## lm(formula = Stress ~ Anxiety + Support, data = stress_df)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.1958 -0.8994 -0.1370  0.9990  3.6995 
## 
## Coefficients:
##             Estimate Std. Error t value         Pr(>|t|)    
## (Intercept) -0.31587    0.85596  -0.369         0.712792    
## Anxiety      0.25609    0.06740   3.799         0.000234 ***
## Support      0.40618    0.05115   7.941 0.00000000000149 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.519 on 115 degrees of freedom
## Multiple R-squared:  0.3556,	Adjusted R-squared:  0.3444 
## F-statistic: 31.73 on 2 and 115 DF,  p-value: 0.00000000001062
```

---

## Suppression

Recall that the partial regression coefficient is calculated:

`$$\large b^*_{Y1.2}=\frac{r_{Y1}-r_{Y2}r_{12}}{1-r^2_{12}}$$`

Is suppression meaningful? 
???

Imagine a scenario when X2 and Y are uncorrelated and X2 is correlated with X1.

(Draw Venn diagram of this)

Second part of numerator becomes 0
Bottom part gets smaller
Bigger value

---

class: inverse

## Next time...

Model comparisons

Categorical predictors